题目内容
若函数y=（2a-4）x+3是增函数，则a的取值范围是 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意可得2a-4＞0，由此求得a的范围．
解答：
解：由函数y=（2a-4）x+3是增函数，可得2a-4＞0，求得a＞2，
故答案为：（2，+∞）．
故答案为：（2，+∞）．
点评：本题主要考查函数的单调性的性质，属于基础题．
练习册系列答案
相关题目
两个正数a，b的等差中项是
，一个等比中项是
，且a＞b，则椭圆
+
=1的离心率e等于（ ）
| 5 |
| 2 |
| 6 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列an=8+
若其最大项和最小项分别为M和m，则m+M的值为（ ）
| 2n-7 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
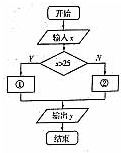某客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过25kg按0.5元/kg收费，超过25kg的部分按0.8元/kg收费，计算收费的程序框图如右图所示，则①②处应填（ ）| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+（x-25）×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |