题目内容
已知F1，F2为椭圆的左右焦点，抛物线以F1为顶点，F2为焦点，设P为椭圆与抛物线的一个交点，椭圆离心率为e，且PF1=ePF2，求e的值．
考点：椭圆的简单性质
专题：计算题,作图题,圆锥曲线的定义、性质与方程
分析：由题意作出其图象，并过点P作椭圆的左准线的垂线，垂足为T，由图象可知，过点P作椭圆的左准线的垂线，垂足为T，椭圆的左准线即为抛物线的准线，从而得到
-c=2c，从而求e．
| a2 |
| c |
解答：
解：如图：
过点P作椭圆的左准线的垂线，垂足为T，
则
=e=
，
则PT=PF2，
则椭圆的左准线即为抛物线的准线，
则AF1=F1F2，即
-c=2c，
则e=
=
．
过点P作椭圆的左准线的垂线，垂足为T，
则
| PF1 |
| PT |
| PF1 |
| PF2 |
则PT=PF2，
则椭圆的左准线即为抛物线的准线，
则AF1=F1F2，即
| a2 |
| c |
则e=
| c |
| a |
| ||
| 3 |
点评：本题考查了椭圆的基本性质的应用，同时考查了学生的作图能力，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
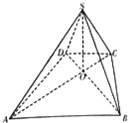如图所示，四棱锥S-ABCD的底面ABCD为等腰梯形，AB∥CD，对角线AC与BD交于点O，OA=3，OD=1，CD=
已知数列{an}满足2an+1+an=0，a1=-2，则数列{an}的前10项和S10为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|