题目内容
如图，在半径为4的⊙O中，∠AOB=90°，D为OB的中点，AD的延长线交⊙O于点E，则线段DE的长为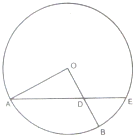 
考点：与圆有关的比例线段
专题：立体几何
分析：延长BO交⊙O与点C，由相交弦定理知AD•DE=BD•DC，由此能求出DE．
解答：
解：
延长BO交⊙O与点C，
由题设知：BD=2，DC=6，AD=
=2
，
又由相交弦定理知AD•DE=BD•DC，
解得DE=
=
=
．
故答案为：
．
延长BO交⊙O与点C，由题设知：BD=2，DC=6，AD=
| 42+22 |
| 5 |
又由相交弦定理知AD•DE=BD•DC，
解得DE=
| BD•DC |
| AD |
| 2×6 | ||
2
|
6
| ||
| 5 |
故答案为：
6
| ||
| 5 |
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意相交弦定理的合理运用．
练习册系列答案
相关题目
已知tanα=
，则
等于（ ）
| 1 |
| 2 |
| cos2α+sin2α+1 |
| cos2α |
| A、4 | ||
| B、6 | ||
| C、12 | ||
D、
|
已知数列{an}满足2an+1+an=0，a1=-2，则数列{an}的前10项和S10为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
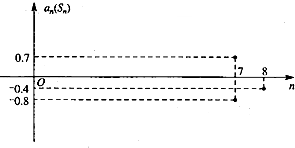设等差数列{an}的前n项和为Sn，在同一个坐标系中，an=f（n）及Sn=g（n）的部分图象如图所示，则（ ）| A、当n=4时，Sn取得最大值 |
| B、当n=3时，Sn取得最大值 |
| C、当n=4时，Sn取得最小值 |
| D、当n=3时，Sn取得最大值 |