题目内容
2.设奇函数f(x)=$\left\{\begin{array}{l}{acosx-\sqrt{3}sinx+c,x≥0}\\{cosx+bsinx-c,x<0}\end{array}\right.$,则a+c的值为0,不等式f(x)>f(-x)在x∈[-π,π]上的解集为[-$\frac{2}{3}π$,$\frac{2}{3}π]$.分析 奇函数,在x=0处有意义,则f(0)=0,算出c=0,在根据奇函数的对称性解题.
解答 解:∵f(x)为奇函数,
∴f(0)=0,f(0)=a+c=0.
∵f(x)>f(-x),
∴f(x)>-f(x),f(x)>0.
∵f(-π)=-f(π),
∴-1-c=a-c,a=-1,c=1,
∵$\sqrt{3}sinx+cosx<1$,
∴$sin(x+\frac{π}{6})<\frac{1}{2}$,[0,π],
故答案为:为[-$\frac{2}{3}π$,$\frac{2}{3}π]$.
点评 奇函数的性质,求出a,和c,先求出[0,π]上的解集,最后根据对称性,求出整个范围.

练习册系列答案
相关题目
10.设函数f(x)=2${\;}^{\sqrt{|x|+1}}$-$\frac{3}{1+{x}^{2}}$,则使得f(x2+$\frac{2}{3}$x+2)>f(-x2+x-1)成立的x的取值范围是( )
| A. | [-$\frac{3}{5}$,+∞) | B. | (-∞,$\frac{3}{5}$] | C. | (-$\frac{3}{5}$,+∞) | D. | $({-\frac{3}{5},\frac{3}{5}})$ |
17.函数y=2sin$\frac{πx}{2}$+1的部分图象如图所示,则(${\overrightarrow{OA}$+2$\overrightarrow{OB}}$)•$\overrightarrow{AB}$=( )
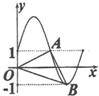

| A. | -10 | B. | -5 | C. | 5 | D. | 10 |
14.已知函数f(x)=$\frac{a(x-1)}{x+1}$-lnx在[1,+∞)上是减函数,则实数a的取值范围为( )
| A. | a<1 | B. | a<2 | C. | a≤2 | D. | a≤3 |
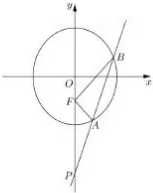 如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P
如图,设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点,直线y=kx-4(k>0)与椭圆相交于A、B两点,与y轴交于点P