题目内容
观察下列等式:
+
i=cos
+isin
,
(
+
i)2=cos
+isin
,
(
+
i)3=cosπ+isiπ,
(
+
i)4=cos
+isin
,
…
照此规律,可以推测对于任意的n∈N*,(
+
i)n= .
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
(
| ||
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
(
| ||
| 2 |
| 1 |
| 2 |
(
| ||
| 2 |
| 1 |
| 2 |
| 4π |
| 3 |
| 4π |
| 3 |
…
照此规律,可以推测对于任意的n∈N*,(
| ||
| 2 |
| 1 |
| 2 |
考点:归纳推理
专题:推理和证明
分析:通过式子的结构特点进行分析,左边是(
+
i)的幂的形式,且次数逐项增加,右边都是同角的余正弦,且角是以
为公差的等差数列,由此可得结果.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
解答:
解:观察可知
等式左边是以(
+
i)为首项,公比为(
+
i)的等比数列,
所以第n行等式左边为(
+
i)n,右边每行都是同角的余弦加正弦,且角是以
为首项,公差为
的等差数列,
所以第n行等式右边为cos
+sin
.
故答案为cos
+isin
等式左边是以(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以第n行等式左边为(
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
所以第n行等式右边为cos
| nπ |
| 3 |
| nπ |
| 3 |
故答案为cos
| nπ |
| 3 |
| nπ |
| 3 |
点评:这是一个考查归纳推理的问题,主要是从式子的结构特点入手分析,例如本题的右端是同角的余弦加正弦,且的角的规律为等差数列,本题不难.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线l过点A(2,4)且与圆x2+y2=4相切,则l的方程是( )
| A、3x-4y+10=0 |
| B、x=2或3x-4y+10=0 |
| C、x-y+2=0 |
| D、x=2或x-y+2=0 |
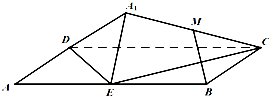 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是