题目内容
已知y=lg(ax-1)-lg(x-1)在(10,+∞)上是增函数,则a的取值范围 .
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:应先满足函数的定义域,即当x∈(10,+∞)时ax-1>0恒成立,由此可得a≥
;然后将原函数化为y=lg
=lg(a+
),结合已知应有y=
在(10,+∞)上递增,结合“反比例”函数的性质可求得a<1 ②最后根据①②可得a的取值范围是[
,1).
| 1 |
| 10 |
| ax-1 |
| x-1 |
| a-1 |
| x-1 |
| a-1 |
| x-1 |
| 1 |
| 10 |
解答:
解:由函数的定义域,即当 x∈(10,+∞)时,ax-1>0恒成立,
显然a>0,∴y=ax-1是增函数,∴只需10a-1≥0,即a≥
①
原函数可化为y=lg
=lg(a+
),
由题意只需y=
在(10,+∞)上递增,结合“反比例”函数的图象性质可知,
只需a-1<0,即a<1 ②
结合①②可得a的取值范围是[
,1).
故答案为:[
,1)
显然a>0,∴y=ax-1是增函数,∴只需10a-1≥0,即a≥
| 1 |
| 10 |
原函数可化为y=lg
| ax-1 |
| x-1 |
| a-1 |
| x-1 |
由题意只需y=
| a-1 |
| x-1 |
只需a-1<0,即a<1 ②
结合①②可得a的取值范围是[
| 1 |
| 10 |
故答案为:[
| 1 |
| 10 |
点评:本题综合考查了函数的单调性(包括反比例函数)的性质,不等式恒成立的问题;不等式恒成立问题一般转化为函数的最值问题来解决,属于一种常考题型,应引起重视.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设
如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设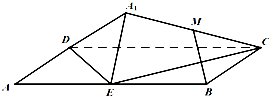 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,正确的命题是