题目内容
“φ=0”是“函数f（x）=sin（x+φ）为奇函数”的 条件．（从“充要”，“充分不必要”，“必要不充分”，“既不充分也不必要”中选择适当的填写）
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据函数奇偶性的定义，结合充分条件和必要条件的定义即可得到结论．
解答：
解：若φ=0，则f（x）=sin（x+φ）=sinx为奇函数，即充分性成立，
若f（x）=sin（x+φ）为奇函数，则φ=kπ，φ=0不一定成立，即必要性不成立，
即“φ=0”是“函数f（x）=sin（x+φ）为奇函数”的充分不必要条件，
故答案为：充分不必要
若f（x）=sin（x+φ）为奇函数，则φ=kπ，φ=0不一定成立，即必要性不成立，
即“φ=0”是“函数f（x）=sin（x+φ）为奇函数”的充分不必要条件，
故答案为：充分不必要
点评：本题主要考查充分条件和必要条件的判断，利用三角函数的奇偶性的性质是解决本题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
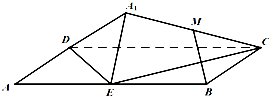如图，矩形ABCD中，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，正确的命题是