题目内容
3.给出下列四个命题:(1)方程x2+y2-2x-1=0表示的是圆;
(2)动点到两个定点的距离之和为一定长,则动点的轨迹为椭圆;
(3)抛物线x=2y2的焦点坐标是$({\frac{1}{8},0})$;
(4)若双曲线$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{k}$=1的离心率为e,且1<a<2,则k的取值范围是k∈(-12,0)
其中正确命题的序号是(1)(3)(4).
分析 (1),(2),(3)可直接根据圆锥曲线的定义进行判断;
(4)可利用离心率的定义得出1<$\frac{\sqrt{4-k}}{2}$<2,求出k的范围.
解答 解:(1)方程x2+y2-2x-1=0可整理为(x-1)2+y2=2表示的是圆,故正确;
(2)动点到两个定点的距离之和为一定长,且大于两顶点间的距离时,则动点的轨迹为椭圆,故错误;
(3)抛物线x=2y2整理得y2=$\frac{1}{2}$x,得焦准距p=$\frac{1}{4}$,得焦点坐标是$({\frac{1}{8},0})$,故正确;
(4)若双曲线$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{k}$=1的离心率为e,且1<e<2,
∴1<$\frac{\sqrt{4-k}}{2}$<2,
∴-12<k<0.故正确.
故答案为(1)(3)(4).
点评 考查了圆锥曲线的定义,焦点坐标,离心率的求解.属于基础题型,应熟练掌握.

练习册系列答案
相关题目
13.已知f(x),g(x),h(x)为R上的函数,其中函数f(x)为奇函数,函数g(x)为偶函数,则( )
| A. | 函数h(g(x))为偶函数 | B. | 函数h(f(x))为奇函数 | C. | 函数g(h(x))为偶函数 | D. | 函数f(h(x))为奇函数 |
18.已知f(x)是定义在[-2,2]上的奇函数,当x∈(0,2]时,f(x)=2x-1,函数g(x)=x2-2x+m,如果对于任意x1∈[-2,2],存在x2∈[-2,2],使得g(x2)=f(x1),则实数m的取值范围是( )
| A. | (-∞,-2) | B. | (-5,-2) | C. | [-5,-2] | D. | (-∞,-2] |
15.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(1,-3),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
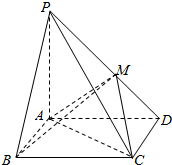 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.