题目内容
已知定义在(0,+∞)上的函数f(x),满足f(xy)=f(x)+f(y),且f(
)=1,对于x,y∈(0,+∞),当且仅当x>y时f(x)<f(y).
(1)求f(1)的值;
(2)若f(-x)+f(3-x)≥-2,求x的取值范围.
| 1 |
| 2 |
(1)求f(1)的值;
(2)若f(-x)+f(3-x)≥-2,求x的取值范围.
考点:抽象函数及其应用,函数单调性的性质
专题:函数的性质及应用
分析:(1)令x=y=1代入f(xy)=f(x)+f(y)可得f(1);
(2)在f(xy)=f(x)+f(y)中给xy取值得出f(4)=-2,把f(-x)+f(3-x)≥-2转化为f[-x(3-x)]≥f(4),利用单调性解不等式.
(2)在f(xy)=f(x)+f(y)中给xy取值得出f(4)=-2,把f(-x)+f(3-x)≥-2转化为f[-x(3-x)]≥f(4),利用单调性解不等式.
解答:
解:(1)∵函数定义在(0,+∞)上,且满足f(xy)=f(x)+f(y),
∴令x=y=1代入上式得f(1)=f(1)+f(1),
∴f(1)=0.
(2)令x=2,y=
代入f(xy)=f(x)+f(y),
f(1)=f(2)+f(
)=f(2)+1,而f(1)=0,
∴f(2)=-1,
令x=2,y=2代入f(xy)=f(x)+f(y),得f(4)=f(2)+f(2)=-2,
∵f(-x)+f(3-x)=f[-x(3-x)]
∴f(-x)+f(3-x)≥-2可化为f[-x(3-x)]≥f(4),
又对于x,y∈(0,+∞),当且仅当x>y时f(x)<f(y),
∴函数f(x)为(0,+∞)上的减函数,
∴
解得-1≤x<0
∴令x=y=1代入上式得f(1)=f(1)+f(1),
∴f(1)=0.
(2)令x=2,y=
| 1 |
| 2 |
f(1)=f(2)+f(
| 1 |
| 2 |
∴f(2)=-1,
令x=2,y=2代入f(xy)=f(x)+f(y),得f(4)=f(2)+f(2)=-2,
∵f(-x)+f(3-x)=f[-x(3-x)]
∴f(-x)+f(3-x)≥-2可化为f[-x(3-x)]≥f(4),
又对于x,y∈(0,+∞),当且仅当x>y时f(x)<f(y),
∴函数f(x)为(0,+∞)上的减函数,
∴
|
点评:本题考查了抽象函数的应用,考查了函数的单调性的判断,训练了特值法求函数的值,考查了学生灵活处理问题和解决问题的能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
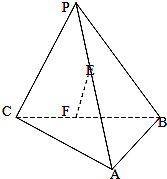 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、120° | B、45° |
| C、0° | D、60° |
设关于x,y的不等式组
表示的平面区域内存在点P(x0,y0),满足x0-3y0=3,求得m的取值范围是( )
|
A、(-∞,-
| ||
B、(-∞,
| ||
C、(-∞,-
| ||
D、(-∞,
|
如果函数y=3cos(2x+φ)的图象关于点(
,0)中心对称,那么ϕ的最小正值为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若a,b,c∈R,a>b,则下列不等式成立的是( )
A、
| ||||
| B、a2>b2 | ||||
C、
| ||||
| D、a|c|>b|c| |
为了得到函数y=sin2x的图象,只需要把函数y=sin(2x+
)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|