题目内容
设f（x）=|lg（x-1）|，若0＜a＜b，且f（a）=f（b），则ab的取值范围是（ ）
| A、[1，2] |
| B、（1，2） |
| C、（4，+∞） |
| D、（2，+∞） |
考点：基本不等式在最值问题中的应用,对数函数的图像与性质
专题：函数的性质及应用
分析：f（x）是含有绝对值的函数，结合函数的图象或通过去绝对值考查f（x）的单调性，找出a和b的关系，结合基本不等式求范围即可．
解答：
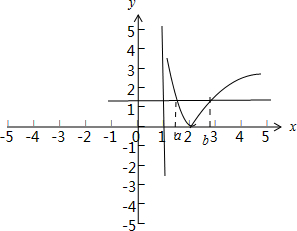解：先画出函数f（x）=|lg（x-1）|的图象，如图：
∵0＜a＜b，且f（a）=f（b），
∴1＜a＜2，b＞2，
∴-lg（a-1）=lg（b-1），
∴
=b-1，
∴a=1+
，
∴ab=b+
=b+
=b-1+
+2＞2
=4，
∴ab的取值范围是（4，+∞），
故选：C
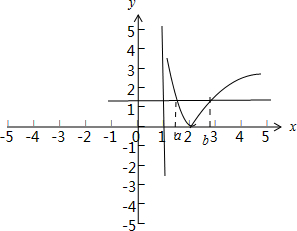解：先画出函数f（x）=|lg（x-1）|的图象，如图：∵0＜a＜b，且f（a）=f（b），
∴1＜a＜2，b＞2，
∴-lg（a-1）=lg（b-1），
∴
| 1 |
| a-1 |
∴a=1+
| 1 |
| b-1 |
∴ab=b+
| b |
| b-1 |
| b-1+1 |
| b-1 |
| 1 |
| b-1 |
(b-1)•
|
∴ab的取值范围是（4，+∞），
故选：C
点评：本题考查函数的性质、基本不等式等，去绝对值是解决本题的关键，综合性强．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知直线l经过两条直线2x-y+6=0和3x+y+4=0的交点
（1）若直线l与直线3x-4y+4=0垂直，求直线l的方程
（2）若直线m与（1）中所求直线l平行，且m与l之间的距离为2，求直线m的方程．
（1）若直线l与直线3x-4y+4=0垂直，求直线l的方程
（2）若直线m与（1）中所求直线l平行，且m与l之间的距离为2，求直线m的方程．
在△ABC中，角A，B，C所对的边分别为a，b，c，已知A=
，a=1，b=
，则B=（ ）
| π |
| 6 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
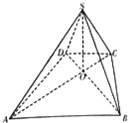如图所示，四棱锥S-ABCD的底面ABCD为等腰梯形，AB∥CD，对角线AC与BD交于点O，OA=3，OD=1，CD=