题目内容
20.中国古代名词“刍童”原来是草堆的意思,古代用它作为长方棱台(上、下底面均为矩形的棱台)的专用术语,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上袤,下袤从之,亦倍下袤,上袤从之,各以其广乘之,皆六而一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘,将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘,把这两个数值相加,与高相乘,再取其六分之一,依此算法,现有上、下底面为相似矩形的棱台,相似比为$\frac{1}{2}$,高为3,其上底面的周长为6,则该棱台的体积的最大值为( )| A. | 14 | B. | 56 | C. | $\frac{63}{4}$ | D. | 63 |
分析 设上底面的长为x,宽为y,则x+y=3,x>0,y>0,由此得到该棱台的体积V=[(2x+2x)y+(4x+x)•2y]×$3×\frac{1}{6}$,利用基本不等式能求出该棱台的体积的最大值.
解答 解:设上底面的长为x,宽为y,则x+y=3,x>0,y>0,
∴该棱台的体积V=[(2x+2x)y+(4x+x)•2y]×$3×\frac{1}{6}$=7xy≤7×($\frac{x+y}{2}$)2=7×$\frac{9}{4}$=$\frac{63}{4}$.
∴该棱台的体积的最大值为$\frac{63}{4}$.
故选:C.
点评 本题考查棱台的体积的最大值的求法,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
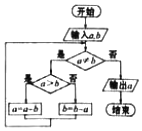 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为98,63,则输出的a为( ) 在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.
在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.