题目内容
1.求与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有共同焦点且过点(3,$\sqrt{2}$)的双曲线的标准方程.分析 由题意知椭圆的焦点坐标为(-2,0),(2,0);从而设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4-{a}^{2}}$=1,代入点(3,$\sqrt{2}$)即可求得.
解答 解:∵椭圆的标准方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1,
∴a=3,c=2,
∴椭圆的焦点坐标为(-2,0),(2,0);
故设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4-{a}^{2}}$=1,
∵双曲线过点(3,$\sqrt{2}$),
∴$\frac{9}{{a}^{2}}$-$\frac{2}{4-{a}^{2}}$=1,
解得,a2=3,
故双曲线的标准方程为$\frac{{x}^{2}}{3}$-y2=1.
点评 本题考查了椭圆的标准方程与双曲线的标准方程的应用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
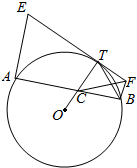 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证: