题目内容

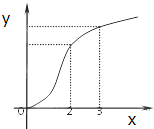已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（　　）
A、0＜f′（2）＜f′（3）＜f（3）-f（2）
B、0＜f′（3）＜f（3）-f（2）＜f′（2）
C、0＜f′（3）＜f′（2）＜f（3）-f（2）
D、0＜f（3）-f（2）＜f′（2）＜f′（3）
考点：函数的图象
专题：作图题,导数的概念及应用
分析：由题意，作出f′（3）、f（3）-f（2）、f′（2）所表示的几何意义，从而求解．
解答： 解：如下图：

f′（3）、f（3）-f（2）、f′（2）分别表示了直线n，m，l的斜率，
故0＜f′（3）＜f（3）-f（2）＜f′（2），
故选B．
点评：本题考查了学生的作图能力及对导数的几何意义的理解，属于中档题．
练习册系列答案
相关题目
若函数满足f（1-x）=f（1+x）且f（0）=3，则f（2）的值为（　　）
A、1B、2C、3D、0
设有复数ω1=-
1
2
+
3
2
i，ω2=cos
2
5
π+isin
2
5
π，令ω=ω1ω2，则复数ω+ω2+ω3+…ω2011=（　　）
A、ω
B、ω2
C、ω1
D、ω2
E、ω
已知a＞0且a≠1，函数y=loga(2x-3)+
2
的图象恒过定点P，若点P在指数函数f（x）的图象上，则f（8）=
 
．
已知直线l过抛物线y=2x2-4x+5的顶点，且倾斜角是α，cosα=
1
3
，求直线l的方程．
已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为
3
2
，两个焦点分别为F1和F2，椭圆G上一点到F1和F2的距离之和为12．圆C：x2+y2+2x-4y-21=0的圆心为点Ak．
（1）求椭圆G的方程；
（2）求△AkF1F2的面积．
设f（x）=2logax，g（x）=loga（5x-6），其中a＞0且a≠1．
（Ⅰ） 若f（x）=g（x），求x的值；
（Ⅱ） 若f（x）＞g（x），求x的取值范围．
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
3
，且它的一个焦点坐标是（1，0），则此椭圆的方程为（　　）
A、
x2
6
+
y2
5
=1
B、
x2
7
+
y2
5
=1
C、
x2
3
+
y2
2
=1
D、
x2
4
+
y2
3
=1
若关于x的不等式ax2+2ax-（a+2）≥0的解集为ϕ，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网