题目内容
设椭圆
+
=1（a＞b＞0）的离心率为
，且它的一个焦点坐标是（1，0），则此椭圆的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：跟进椭圆的几何性质，求出c=1，a=
，b=
，求解方程即可．
| 3 |
| 2 |
解答：
解：∵椭圆
+
=1（a＞b＞0）的离心率为
，且它的一个焦点坐标是（1，0），
∴
=
，c=1，a=
，b=
，
∴椭圆的方程为
+
=1，
故选：C
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
∴
| c |
| a |
| ||
| 3 |
| 3 |
| 2 |
∴椭圆的方程为
| x2 |
| 3 |
| y2 |
| 2 |
故选：C
点评：本题考查了椭圆的几何性质，属于容易题，计算题．
练习册系列答案
相关题目
平面向量
，
的夹角为60°，
=（2，0），|
|=1，则|
+2
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
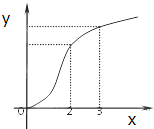已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）| A、0＜f′（2）＜f′（3）＜f（3）-f（2） |
| B、0＜f′（3）＜f（3）-f（2）＜f′（2） |
| C、0＜f′（3）＜f′（2）＜f（3）-f（2） |
| D、0＜f（3）-f（2）＜f′（2）＜f′（3） |
一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是（1，0，0），（0，0，1），（0，1，0），（1，1，1），画该四面体三视图中的正视图时，以zOy平面为投影面，则得到的正视图可为（ ）
A、 |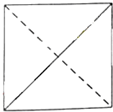
B、 |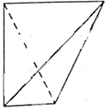
C、 |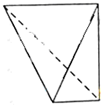
D、 |
| A | 2 8 |
| A、10 | B、30 | C、56 | D、120 |