题目内容
若函数满足f（1-x）=f（1+x）且f（0）=3，则f（2）的值为（ ）
| A、1 | B、2 | C、3 | D、0 |
考点：函数的值
专题：函数的性质及应用
分析：根据f（1-x）=f（1+x），令x=1得f（0）=f（2）=3．
解答：
解：∵f（1-x）=f（1+x），
∴当x=1时有
f（1-1）=f（1+1）
即f（0）=f（2）=3
故选C．
∴当x=1时有
f（1-1）=f（1+1）
即f（0）=f（2）=3
故选C．
点评：本题考查求抽象函数的函数值，常用赋值法，属于一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
P={（x，y）|x+y=5，x∈N*，y∈N*}，则集合的非空子集的个数是（ ）
| A、3 | B、4 | C、15 | D、16 |
若实数x，y满足
，则z=y-x的最小值为（ ）
|
| A、8 | B、-8 | C、-6 | D、6 |
若直线（m+2）x+3y+3=0与直线x+（2m-1）y+m=0平行，则实数m=（ ）
A、-
| ||
| B、1 | ||
| C、1或2 | ||
D、-
|
如图，在正方体ABCD-A1B1C1D1中，AC与A1D所在直线所成的角等于（ ）
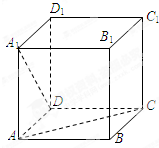
| A、30° | B、45° |
| C、60° | D、90° |
一块电路板的AB线段之间有60个串联的焊接点，知道电路不通的原因是焊口脱落造成的．要想用二分法的思想检测出哪处焊口脱落．至少需要检测（ ）
| A、4次 | B、6次 | C、8次 | D、30次 |
平面向量
，
的夹角为60°，
=（2，0），|
|=1，则|
+2
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
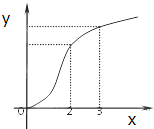已知函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）| A、0＜f′（2）＜f′（3）＜f（3）-f（2） |
| B、0＜f′（3）＜f（3）-f（2）＜f′（2） |
| C、0＜f′（3）＜f′（2）＜f（3）-f（2） |
| D、0＜f（3）-f（2）＜f′（2）＜f′（3） |