题目内容
已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为
,两个焦点分别为F1和F2,椭圆G上一点到F1和F2的距离之和为12.圆C:x2+y2+2x-4y-21=0的圆心为点Ak.
(1)求椭圆G的方程;
(2)求△AkF1F2的面积.
| ||
| 2 |
(1)求椭圆G的方程;
(2)求△AkF1F2的面积.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)椭圆G的标准方程为
+
=1,(a>b>0),求解a,b 即可.(2)利用面积公式求解;点A1到x轴的距离为2,△A1F1F2的面积为
|F1F2|×2,代入求解即可.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
解答:
解:(1)设椭圆G的标准方程为
+
=1,(a>b>0),
则2a=12,所以a=6,
因为离心率为
,
所以c=a•e=3
.b2=a2-c2=9,
所以椭圆G的标准方程为
+
=1,
(2)圆C:x2+y2+2x-4y-21=0的方程化为(x+1)2+(y-2)2=25,
所以点A1的坐标为(-1,2).
点A1到x轴的距离为2,
△A1F1F2的面积为
|F1F2|×2=×2a•2=a=6.
| x2 |
| a2 |
| y2 |
| b2 |
则2a=12,所以a=6,
因为离心率为
| ||
| 2 |
所以c=a•e=3
| 3 |
所以椭圆G的标准方程为
| x2 |
| 36 |
| y2 |
| 9 |
(2)圆C:x2+y2+2x-4y-21=0的方程化为(x+1)2+(y-2)2=25,
所以点A1的坐标为(-1,2).
点A1到x轴的距离为2,
△A1F1F2的面积为
| 1 |
| 2 |
点评:本题考察了椭圆的性质,方程,定义,属于中档题,有点难度.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
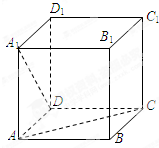
如图,在正方体ABCD-A1B1C1D1中,AC与A1D所在直线所成的角等于( )

| A、30° | B、45° |
| C、60° | D、90° |
函数y=log
(x-3)的定义域为( )
| 1 |
| 2 |
| A、(3,+∞) |
| B、[3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |
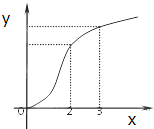 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、0<f′(2)<f′(3)<f(3)-f(2) |
| B、0<f′(3)<f(3)-f(2)<f′(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
 据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )| A、4320 | B、2880 |
| C、8640 | D、2160 |
一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,0),(0,0,1),(0,1,0),(1,1,1),画该四面体三视图中的正视图时,以zOy平面为投影面,则得到的正视图可为( )
A、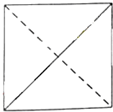 |
B、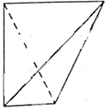 |
C、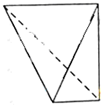 |
D、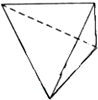 |
| A | 2 8 |
| A、10 | B、30 | C、56 | D、120 |
圆x2+y2-2x-2y+1=0和圆x2+y2-8x-10y+25=0的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、相离 |
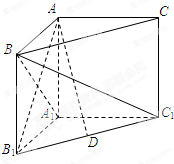 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.