题目内容
已知a>0且a≠1,函数y=loga(2x-3)+
的图象恒过定点P,若点P在指数函数f(x)的图象上,则f(8)= .
| 2 |
考点:指数函数的单调性与特殊点
专题:函数的性质及应用
分析:由题意求出点P的坐标,代入f(x)求函数解析式,再将8代入即可.
解答:
解:由题意,令2x-3=1,即x=2,则y=
,
即点P(2,
),
由P在指数函数f(x)的图象上可得,
=a2,
则a=2
,
则f(x)=(2
)x,
则f(8)=(2
)8=4,
故答案为:4
| 2 |
即点P(2,
| 2 |
由P在指数函数f(x)的图象上可得,
| 2 |
则a=2
| 1 |
| 4 |
则f(x)=(2
| 1 |
| 4 |
则f(8)=(2
| 1 |
| 4 |
故答案为:4
点评:本题考查了对数函数与指数函数的性质应用,属于基础题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
若实数x,y满足
,则z=y-x的最小值为( )
|
| A、8 | B、-8 | C、-6 | D、6 |
平面向量
,
的夹角为60°,
=(2,0),|
|=1,则|
+2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、2
| ||||
B、
| ||||
C、
| ||||
| D、2 |
函数y=log
(x-3)的定义域为( )
| 1 |
| 2 |
| A、(3,+∞) |
| B、[3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |
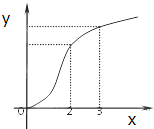 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、0<f′(2)<f′(3)<f(3)-f(2) |
| B、0<f′(3)<f(3)-f(2)<f′(2) |
| C、0<f′(3)<f′(2)<f(3)-f(2) |
| D、0<f(3)-f(2)<f′(2)<f′(3) |
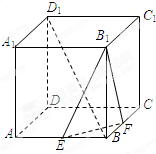 如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别是AB、BC的中点.
如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别是AB、BC的中点.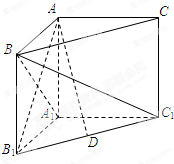 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.