题目内容
9.抛物线y2=2px(p>0)的焦点为F,直线l过焦点F且斜率为2,与抛物线交于A、B(其中A在第一象限)两点,M(-$\frac{p}{2}$,0),则tan∠AMF=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2}{5}$$\sqrt{5}$ |
分析 根据直线l的斜率k=2,设出A的坐标,代入抛物线y2=2px,求出A的坐标,从而可求tan∠AMF.
解答 解:∵直线l的斜率k=2,
∴可设A($\frac{p}{2}$+y,2y),代入抛物线y2=2px,可得4y2=2p($\frac{p}{2}$+y),
∴y=$\frac{1+\sqrt{5}}{4}$p,
∴tan∠ANF=$\frac{2y}{p+y}$=$\frac{\frac{2+2\sqrt{5}}{4}}{1+\frac{1+\sqrt{5}}{4}}$=$\frac{2\sqrt{5}}{5}$.
故选:D.
点评 本题考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
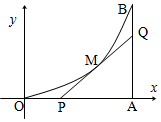 如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.
如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线OB弧上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围城的三角形PQA的面积最大,并求得最大值.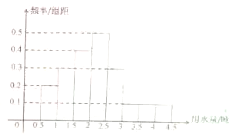 某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.
某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.