题目内容
3.在△ABC中,D为边BC上一点,且AD⊥BC,若AD=1,BD=2,CD=3,则∠BAC的度数为135°.分析 由题意,AB=$\sqrt{5}$,AC=$\sqrt{10}$,BC=5,由余弦定理可得∠BAC的度数.
解答 解:由题意,AB=$\sqrt{5}$,AC=$\sqrt{10}$,BC=5,
由余弦定理可得cos∠BAC=$\frac{5+10-25}{2•\sqrt{5}•\sqrt{10}}$=-$\frac{\sqrt{2}}{2}$,
∵0°<∠BAC<180°
∴∠BAC=135°,
故答案为135°.
点评 本题考查余弦定理、勾股定理的运用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
13.过抛物线y2=2px(p>0)的焦点作倾斜角为$\frac{π}{3}$的直线交抛物线于A,B两点,若|AB|=6,则焦点弦中大小为$\frac{9}{2}$的有几条( )
| A. | 1条 | B. | 2条 | C. | 0条 | D. | 以上都有可能 |
8.直线y=x的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
15.如图是一个四棱锥的三视图,在所有侧面中直角三角形的个数有( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
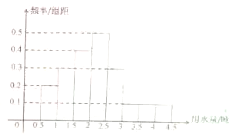 某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.
某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.