题目内容
7.若变量x,y满足约束条件$\left\{\begin{array}{l}2x+y-2\;≥\;0\;\\ x+y-2\;≤\;0\;\\ x-y\;≥\;0\;\end{array}\right.$则$\frac{y}{2x+1}$的最大值为$\frac{1}{3}$.分析 由约束条件作出可行域,再由$\frac{y}{2x+1}$的几何意义,即可行域内的动点与定点P($-\frac{1}{2}$,0)连线的斜率的一半求解.
解答 解:由约束条件$\left\{\begin{array}{l}2x+y-2\;≥\;0\;\\ x+y-2\;≤\;0\;\\ x-y\;≥\;0\;\end{array}\right.$作出可行域如图,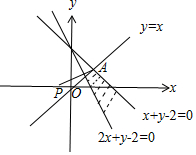
联立$\left\{\begin{array}{l}{y=x}\\{x+y-2=0}\end{array}\right.$,解得A(1,1).
由$\frac{y}{2x+1}$=$\frac{1}{2}•\frac{y-0}{x-(-\frac{1}{2})}$,
而$\frac{y-0}{x-(-\frac{1}{2})}$的几何意义为可行域内的动点与定点P($-\frac{1}{2}$,0)连线的斜率.
且${k}_{PA}=\frac{1-0}{1-(-\frac{1}{2})}=\frac{2}{3}$,
∴$\frac{y}{2x+1}$的最大值为$\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法与数学转化思想方法,属中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.如图是一个四棱锥的三视图,在所有侧面中直角三角形的个数有( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
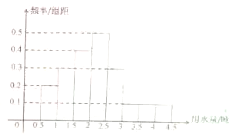 某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.
某城市100户居民的月平均用水量(单位:吨),按[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5)分组的频率分布直方图如图.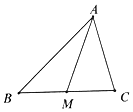 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.