若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一条渐近线与直线3x-y+1=0平行.则此双曲线的离心率是( )A．$\sqrt{3}$B．$2\sqrt{2}$C．3D．$\sqrt{10}$ 题目和参考答案——青夏教育精英家教网—

题目内容

10．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一条渐近线与直线3x-y+1=0平行，则此双曲线的离心率是（　　）

A．

$\sqrt{3}$

B．

$2\sqrt{2}$

C．

D．

$\sqrt{10}$

分析根据双曲线的一条渐近线与直线3x-y+1=0平行，得b=3a，再由双曲线基本量的平方关系，得出a、c的关系式，结合离心率的定义，可得该双曲线的离心率．

解答解：∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的一条渐近线与直3x-y+1=0平行
∴双曲线的渐近线方程为y=±3x
∴$\frac{b}{a}$=3，得b=3a，c=$\sqrt{10}$a
此时，离心率e=$\frac{c}{a}$=$\sqrt{10}$．
故选：D．

点评本题给出双曲线的渐近线方程，求双曲线的离心率，考查了双曲线的标准方程与简单几何性质等知识，属于基础题．

练习册系列答案

1．

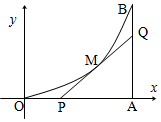如图，由y=0，x=8，y=x²围成的曲边三角形，在曲线OB弧上求一点M，使得过M所作的y=x²的切线PQ与OA，AB围城的三角形PQA的面积最大，并求得最大值．

18．

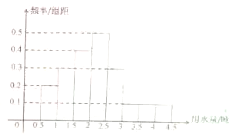某城市100户居民的月平均用水量（单位：吨），按[0.5，1），[1，1.5），[1.5，2），[2，2.5），[2.5，3），[3，3.5），[3.5，4），[4，4.5）分组的频率分布直方图如图．
（1）求月平均用水量的众数和中位数；
（2）在月平均用水量为[1.5，2），[2，2.5），[2.5，3）的三组用户中，用分层抽样的方法抽取12户居民参加用水价格听证会，则月平均用水量在[2，2.5）的用户中应抽取多少户？

5．若锐角α，β满足cos²α+cos²β=1，则$cos\frac{α+β}{2}$=$\frac{\sqrt{2}}{2}$．

15．如图是一个四棱锥的三视图，在所有侧面中直角三角形的个数有（　　）

2．设a＞0，若${（{{x^2}+\frac{a}{{\sqrt{x}}}}）^5}$展开式中的常数项为80，则a=2．

19．已知数列{a_n}的前n项和为S_n，且$\frac{1}{{{a_n}+1}}=\frac{2}{{{a_{n+1}}+1}}，{a_2}=1$，则S₇=120．

20．曲线的极坐标方程为ρ=2cosθ，则曲线的直角坐标方程为（　　）

试题分类