题目内容
7. 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
分析 由|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,根据切线长定理,可得|PF1|-|PF2|=2,结合|F1F2|=4,即可得出结论.
解答 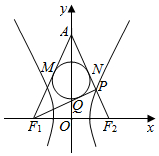 解:∵双曲线的焦距为4,
解:∵双曲线的焦距为4,
∴|F1F2|=4,∴c=2
∵|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,
∴根据切线长定理可得AM=AN,F1M=F1Q,PN=PQ,
∵|AF1|=|AF2|,
∴AM+F1M=AN+PN+NF2,
∴F1M=PN+NF2=PQ+PF2
∴|PF1|-|PF2|=F1Q+PQ-PF2=F1M+PQ-PF2=PQ+PF2+PQ-PF2=2PQ=2,
即2a=2,则a=1,
∵a=1,c=2
∴双曲线的离心率是e=$\frac{c}{a}$=2.
故答案为:2
点评 本题主要考查双曲线的离心率,考查三角形内切圆的性质,考查切线长定理,考查学生的计算能力,利用双曲线的定义进行转化是解决本题的关键.

练习册系列答案
相关题目
17.$({x+\frac{1}{x}}){({2x-\frac{1}{x}})^5}$是展开式的常数项为( )
| A. | 120 | B. | 40 | C. | -40 | D. | 80 |
2.设等差数列{an}满足(1-a1008)5+2016(1-a1008)=1,(1-a1009)5+2016(1-a1009)=-1,数列{an}的前n项和记为Sn,则( )
| A. | S2016=2016,a1008>a1009 | B. | S2016=-2016,a1008>a1009 | ||
| C. | S2016=2016,a1008<a1009 | D. | S2016=-2016,a1008<a1009 |