题目内容
3.函数f(x)=2x-1+log2x的零点所在的一个区间是($\frac{1}{2}$,1).分析 根据函数f(x)=2x-1+log2x,在(0,+∞)单调递增,f(1)=1,f($\frac{1}{2}$)=-1,可判断分析.
解答 解:∵函数f(x)=2x-1+log2x,在(0,+∞)单调递增.
∴f(1)=1>0,f($\frac{1}{2}$)=-1<0,
∴根据函数的零点的判断方法得出:零点所在的一个区间是($\frac{1}{2}$,1),
故答案为:($\frac{1}{2}$,1).
点评 本题考查了函数的性质,函数的零点的判断方法,属于容易题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若$cosα=-\frac{3}{5}$,且$α∈[{\frac{π}{2},π}]$,则$cos({α-\frac{π}{4}})$=( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
13.在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,P是三角形BDC'内的动点,EP⊥BC',则P的轨迹长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
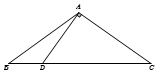 如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3. 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2. 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.