题目内容
18.若a≥0,试讨论函数g(x)=lnx+ax2-(2a+1)x在(0,+∞)上的单调性.分析 求出函数的导函数,求得导函数的零点,然后对a分类分析导函数在各区间段内的符号,得到原函数的单调区间.
解答 解:$g'(x)=\frac{{2a{x^2}-(2a+1)x+1}}{x}$=$\frac{(2ax-1)(x-1)}{x}$.
∵函数g(x)的定义域为(0,+∞),
∴当a=0时,$g'(x)=-\frac{x-1}{x}$,
由g'(x)>0,得0<x<1,由g'(x)<0,得x>1.
即函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当a>0时,令g'(x)=0,得x=1或$x=\frac{1}{2a}$.
若$\frac{1}{2a}<1$,即$a>\frac{1}{2}$时,
由g'(x)>0,得x>1或$0<x<\frac{1}{2a}$,由g'(x)<0,得$\frac{1}{2a}<x<1$.
即函数g(x)在$(0,\frac{1}{2a})$,(1,+∞)上单调递增,在$(\frac{1}{2a},1)$单调递减;
若$\frac{1}{2a}>1$,即$0<a<\frac{1}{2}$时,
由g'(x)>0,得$x>\frac{1}{2a}$或0<x<1,由g'(x)<0,得$1<x<\frac{1}{2a}$.
即函数g(x)在(0,1),$(\frac{1}{2a},+∞)$上单调递增,在$(1,\frac{1}{2a})$单调递减;
若$\frac{1}{2a}=1$,即$a=\frac{1}{2}$时,在(0,+∞)上恒有g'(x)≥0.
即函数g(x)在(0,+∞)上单调递增.
综上所述:
当a=0时,函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当$0<a<\frac{1}{2}$时,函数g(x)在(0,1)上单调递增,
在$(1,\frac{1}{2a})$单调递减;在$(\frac{1}{2a},+∞)$上单调递增;
当$a=\frac{1}{2}$时,函数g(x)在(0,+∞)上单调递增,
当$a>\frac{1}{2}$时,函数g(x)在$(0,\frac{1}{2a})$上单调递增,
在$(\frac{1}{2a},1)$单调递减;在(1,+∞)上单调递增.
点评 本题考查利用导数研究函数的单调性,考查分类讨论的数学思想方法,是中档题.

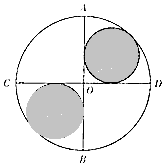 如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )
如图所示,已知AB,CD是圆O中两条互相垂直的直径,两个小圆与圆O以及AB,CD均相切,则往圆O内投掷一个点,该点落在阴影部分的概率为( )| A. | 12-8$\sqrt{2}$ | B. | 3-2$\sqrt{2}$ | C. | 8-5$\sqrt{2}$ | D. | 6-4$\sqrt{2}$ |
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
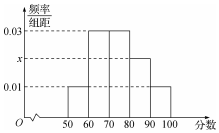 2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).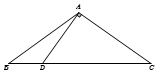 如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3.
如图,在△ABC中,已知点D在BC边上,AD⊥AC,AB=2$\sqrt{5}$,sin∠BAC=$\frac{{\sqrt{5}}}{3}$,AD=3,则BD的长为3. 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为2.