题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
<φ<
)与y=-sinx的图象关于直线
对称.
(1)求函数y=f(x)的表达式;
(2)若将函数f(x)的图象向左平移m(m>0)单位后,图象关于y轴对称,求m的最小值;
(3)将函数y=f(x)的图象上的各点的横坐标缩短为原来的
(纵坐标不变),得到函数y=h(x)的图象,若关于x的方程g(x)+m=0在区间[0,
]上有且只有一个实数解,求实数m的取值范围.
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
(1)求函数y=f(x)的表达式;
(2)若将函数f(x)的图象向左平移m(m>0)单位后,图象关于y轴对称,求m的最小值;
(3)将函数y=f(x)的图象上的各点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,根的存在性及根的个数判断
专题:三角函数的图像与性质
分析:(1)根据对称性直接求解其解析式.
(2)平移后由函数为偶函数得到m-
=kπ+
,由此可求最小正数m的值.
(3)由图象变化法则可得g(x)=sin(2x-
),问题等价于函数g(x)的图象与y=-m只有一个公共点,数形结合可得.
(2)平移后由函数为偶函数得到m-
| π |
| 3 |
| π |
| 2 |
(3)由图象变化法则可得g(x)=sin(2x-
| π |
| 3 |
解答:
解:(1)∵函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
<φ<
)与y=-sinx的图象关于直线
对称.
∴Asin[ω(
-x)+φ]=-sinx,
∴-Asin(ωx-
-φ)=-sinx,
∴可解得:A=1,ω=1,φ=-
,
∴y=f(x)=sin(x-
),
(2)∴将函数y=sin(x-
)的图象向左平移m(m>0)个长度单位后,所得到的图象对应的函数解析式为y=sin(x+m-
).
∵所得到的图象关于y轴对称,
∴y=sin(x+m-
)为偶函数.
即m-
=kπ+
,m=kπ+
.
当k=0时,m的最小值为
.
(3)将函数y=f(x)的图象上各点的横坐标缩短为原来的
倍,纵坐标不变,得到函数y=g(x)的图象.
∴g(x)=sin(2x-
),可得g(x)在[0,
]单调递增,在[
,
]单调递减,
其图象如图所示,
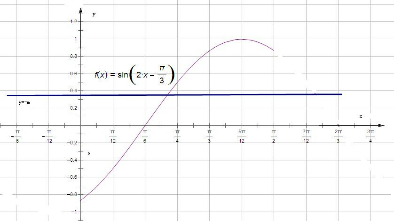
关于x的方程g(x)+m=0在区间[0,
]上有且只有一个实数解,
等价于函数g(x)的图象与y=-m只有一个公共点,
由图象可得-m=1,或-
≤-m<
,
∴实数m的取值范围为:m=-1或-
<m≤
.
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
∴Asin[ω(
| π |
| 3 |
∴-Asin(ωx-
| πω |
| 3 |
∴可解得:A=1,ω=1,φ=-
| π |
| 3 |
∴y=f(x)=sin(x-
| π |
| 3 |
(2)∴将函数y=sin(x-
| π |
| 3 |
| π |
| 3 |
∵所得到的图象关于y轴对称,
∴y=sin(x+m-
| π |
| 3 |
即m-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
当k=0时,m的最小值为
| 5π |
| 6 |
(3)将函数y=f(x)的图象上各点的横坐标缩短为原来的
| 1 |
| 2 |
∴g(x)=sin(2x-
| π |
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
其图象如图所示,
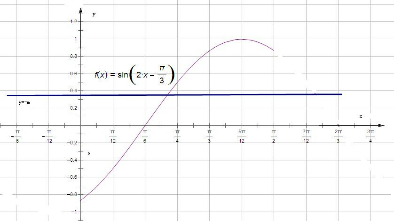
关于x的方程g(x)+m=0在区间[0,
| π |
| 2 |
等价于函数g(x)的图象与y=-m只有一个公共点,
由图象可得-m=1,或-
| ||
| 2 |
| ||
| 2 |
∴实数m的取值范围为:m=-1或-
| ||
| 2 |
| ||
| 2 |
点评:本题重点考查了三角函数的图象与性质、三角函数诱导公式等知识,属于中档题.解题的关键是灵活运用对称思想求解函数的解析式.

练习册系列答案
相关题目
设集合A={x|-1<x≤2,x∈N},集合B={2,3},则A∪B等于( )
| A、{2} |
| B、{1,2,3} |
| C、{-1,0,1,2,3} |
| D、{0,1,2,3} |
某单位2015年元旦联欢晚会准备有歌曲,戏曲,魔术,小品,相声,舞蹈,杂技这7个表演节目,其中歌曲必须放在最后,魔术师表示如果和相声或小品节目相邻时,魔术表演极易出现失误,则尽可能促使魔术表演成功的节目安排的种数有.
| A、288 | B、432 |
| C、576 | D、720 |
 如图,在△ABC中,AD⊥AB,BC=
如图,在△ABC中,AD⊥AB,BC=| 3 |
| AD |
| AC |
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<