题目内容
在区间[-4,4]内任取两个实数a,b,则使函数f(x)=x2+
x+b有零点的概率为 .
| a |
考点:几何概型
专题:概率与统计
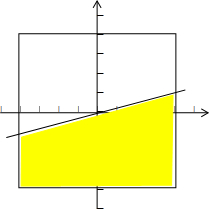
分析:根据题意,以a为横坐标、b为纵坐标建立如图所示直角坐标系,得到所有的点在如图的正方形OABC及其内部任意取,由一元二次方程根与系数的关系,算出函数f(x)=x2+
x+b有零点时满足a≥4b,满足条件的点(a,b)在正方形内部且在直线a-4b=0的下方,因此可得阴影面积除以正方形的面积,即可得到所求的概率.
| a |
解答:
 解:∵两个数a、b在区间[-4,4]内随地机取,
解:∵两个数a、b在区间[-4,4]内随地机取,
∴以a为横坐标、b为纵坐标建立如图所示直角坐标系,
若函数f(x)=x2+
x+b有零点,则
△=a-4b≥0,解之得a≥4b,满足条件的点(a,b)在直线a-4b=0的下方,且在正方形内部,
其面积为S1=
×[(-1)-(-4)+1-(-4)]×[4-(-4)]=32
∵正方形的面积为S=8×8=64
∴函数f(x)=x2+
x+b有零点的概率为P=
=
,
故答案为:
 解:∵两个数a、b在区间[-4,4]内随地机取,
解:∵两个数a、b在区间[-4,4]内随地机取,∴以a为横坐标、b为纵坐标建立如图所示直角坐标系,
若函数f(x)=x2+
| a |
△=a-4b≥0,解之得a≥4b,满足条件的点(a,b)在直线a-4b=0的下方,且在正方形内部,
其面积为S1=
| 1 |
| 2 |
∵正方形的面积为S=8×8=64
∴函数f(x)=x2+
| a |
| S1 |
| S |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题给出a、b满足的关系式,求函数f(x)=x2+
x+b有零点的概率,着重考查了面积计算公式、一元二次方程根的判别式和几何概型计算公式等知识,属于基础题.
| a |

练习册系列答案
相关题目
设函数f(x)=x2-ax+b,a,b∈R.
(1)已知f(x)在区间(-∞,1)上单调递减,求a的取值范围;
(2)存在实数a,使得当x∈[0,b]时,2≤f(x)≤6恒成立,求b的最大值及此时a的值.
(1)已知f(x)在区间(-∞,1)上单调递减,求a的取值范围;
(2)存在实数a,使得当x∈[0,b]时,2≤f(x)≤6恒成立,求b的最大值及此时a的值.
(理)已知函数f(x)是定义在实数集R上的以2为周期的偶函数,当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图象在[0,2]内恰有两个不同的公共点,则实数a的值是( )
A、-
| ||||
| B、0 | ||||
C、0或-
| ||||
D、0或-
|
 如图,椭圆
如图,椭圆