题目内容
设△ABC的内角A，B，C所对的边长分别为a，b，c，且cosB=
，b=2，
（1）当A=30°时，求a的值；
（2）当△ABC的面积为3时，求a，c的值．
| 4 |
| 5 |
（1）当A=30°时，求a的值；
（2）当△ABC的面积为3时，求a，c的值．
考点：正弦定理
专题：解三角形
分析：（1）根据cosB求得sinB，进而利用正弦定理求得a．
（2）利用三角形面积公式求得ac的值，进而利用余弦定理求得a+c的值，最后联立方程求得a和c．
（2）利用三角形面积公式求得ac的值，进而利用余弦定理求得a+c的值，最后联立方程求得a和c．
解答：
解：（1）∵△ABC中，cosB=
，
∴sinB=
=
，
由正弦定理知
=
，
∴a=
•sinA=
×
=
．
（2）由S△ABC=
acsinB=
ac=3，
∴ac=10 ①
∵cosB=
=
=
=
∴（a+c）2=40，
∴a+c=2
②
由①②得：a=
，c=
．
| 4 |
| 5 |
∴sinB=
| 1-cos2B |
| 3 |
| 5 |
由正弦定理知
| a |
| sinA |
| b |
| sinB |
∴a=
| b |
| sinB |
| 2 | ||
|
| 1 |
| 2 |
| 5 |
| 3 |
（2）由S△ABC=
| 1 |
| 2 |
| 3 |
| 10 |
∴ac=10 ①
∵cosB=
| a2+c2-b2 |
| 2ac |
| (a+c)2-2ac-b2 |
| 2ac |
| (a+c)2-24 |
| 20 |
| 4 |
| 5 |
∴（a+c）2=40，
∴a+c=2
| 10 |
由①②得：a=
| 10 |
| 10 |
点评：本题主要考查了正弦定理和余弦定理的应用．正弦定理和余弦定理是解三角函数常用的方法，应熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
在[0，2π]上满足cos（
-α）≥
的α取值范围是（ ）
| 5π |
| 2 |
| 1 |
| 2 |
A、[0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知角α终边上异于原点一点P且|PO|=r，则P点坐标为（ ）
| A、P（sinα，cosα） |
| B、P（cosα，sinα） |
| C、P（rsinα，rcosα） |
| D、P（rcosα，rsinα） |
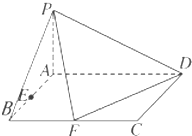已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是线段AB，BC的中点，
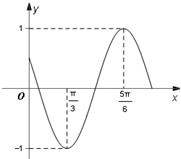已知函数f（x）=cos（ωx+φ）（ω＞0，0＜φ＜