题目内容
抛物线C1的顶点在原点焦点在y轴上,且经过点P(2,2),圆C2过定点A(0,1),且圆心C2在抛物线C1上,记圆C2与x轴的两个交点为M、N.
(1)求抛物线C1的方程;
(2)当圆心C2在抛物线上运动时,试问|MN|是否为一定值?请证明你的结论;
(3)当圆心C2在抛物线上运动时,记|AM|=m,|AN|=n,求
+
的最大值.
(1)求抛物线C1的方程;
(2)当圆心C2在抛物线上运动时,试问|MN|是否为一定值?请证明你的结论;
(3)当圆心C2在抛物线上运动时,记|AM|=m,|AN|=n,求
| m |
| n |
| n |
| m |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出抛物线方程,代入P,即可求出抛物线的方程;
(2)表示出圆被x轴截得的弦长,利用圆心在抛物线上,即可得出结论;
(3)表示出
+
,分类讨论,利用基本不等式,即可求出最大值.
(2)表示出圆被x轴截得的弦长,利用圆心在抛物线上,即可得出结论;
(3)表示出
| m |
| n |
| n |
| m |
解答:
解:(1)由已知,设抛物线方程为x2=2py,则
代入P(2,2),可得p=1,
∴抛物线C1的方程为x2=2y;
(2)设圆的圆心C2(a,b),则圆的半径为
,
∴圆被x轴截得的弦长为|MN|=2
=2
=2
,
∵a2=2b,
∴|MN|=2;
(3)由(2)知,不妨设M(a-1,0),N(a+1,0),则
m=
=
,n=
=
,
∴
+
=
=2
.
a=0时,
+
=2;
a≠0时,
+
=2
≤2
,当且仅当a=±
时,
+
取得最大值2
.
代入P(2,2),可得p=1,
∴抛物线C1的方程为x2=2y;
(2)设圆的圆心C2(a,b),则圆的半径为
| a2+(b-1)2 |
∴圆被x轴截得的弦长为|MN|=2
| r2-b2 |
| a2+b2-2b+1-b2 |
| a2-2b+1 |
∵a2=2b,
∴|MN|=2;
(3)由(2)知,不妨设M(a-1,0),N(a+1,0),则
m=
| (a-1)2+1 |
| a2+2-2a |
| (a+1)2+1 |
| a2+2+2a |
∴
| m |
| n |
| n |
| m |
| 2a2+4 | ||
|
1+
|
a=0时,
| m |
| n |
| n |
| m |
a≠0时,
| m |
| n |
| n |
| m |
1+
|
| 2 |
| 2 |
| m |
| n |
| n |
| m |
| 2 |
点评:待定系数法是求圆锥曲线的常用方法,利用基本不等式可以解决最值问题.

练习册系列答案
相关题目
若函数f(x+1)=
,则f(4)=( )
| x | ||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
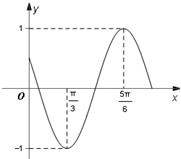 已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<
已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<

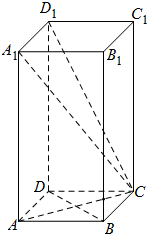 已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.
已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.