题目内容
在数列{an}中,an=
(n∈N*).从数列{an}中选出k(k≥3)项并按原顺序组成的新数列记为{bn},并称{bn}为数列{an}的k项子列.例如数列
,
,
,
为{an}的一个4项子列.
(Ⅰ)试写出数列{an}的一个3项子列,并使其为等差数列;
(Ⅱ)如果{bn}为数列{an}的一个5项子列,且{bn}为等差数列,证明:{bn}的公差d满足-
<d<0;
(Ⅲ)如果{cn}为数列{an}的一个m(m≥3)项子列,且{cn}为等比数列,证明:c1+c2+c3+…+cm≤2-
.
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 8 |
(Ⅰ)试写出数列{an}的一个3项子列,并使其为等差数列;
(Ⅱ)如果{bn}为数列{an}的一个5项子列,且{bn}为等差数列,证明:{bn}的公差d满足-
| 1 |
| 8 |
(Ⅲ)如果{cn}为数列{an}的一个m(m≥3)项子列,且{cn}为等比数列,证明:c1+c2+c3+…+cm≤2-
| 1 |
| 2m-1 |
考点:数列与不等式的综合,等差关系的确定,等差数列的性质
专题:新定义,等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)根据新定义的规定,从原数列中找出符合条件的一个数列,注意本题答案不唯一;
(Ⅱ)先利用反证法推出新数列的第一项不等于1,再利用等差数列中项与项的关系,得到公差的取值范围;
(Ⅲ)对于新数列,先研究其首项,再利用公比是有理数,对公比进行分类研究,得到本题的结论.
(Ⅱ)先利用反证法推出新数列的第一项不等于1,再利用等差数列中项与项的关系,得到公差的取值范围;
(Ⅲ)对于新数列,先研究其首项,再利用公比是有理数,对公比进行分类研究,得到本题的结论.
解答:
(Ⅰ)解:答案不唯一.如3项子列
,
,
;
(Ⅱ)证明:由题意,知1≥b1>b2>b3>b4>b5>0,
所以d=b2-b1<0.
假设b1=1,
由{bn}为{an}的一个5项子列,得b2≤
,
所以d=b2-b1≤
-1=-
.
因为b5=b1+4d,b5>0,
所以4d=b5-b1=b5-1>-1,即d>-
.
这与d≤-
矛盾.
所以假设不成立,即b1≠1.
所以b1≤
,
因为b5=b1+4d,b5>0,
所以4d=b5-b1≥b5-
>-
,即d>-
,
综上,得-
<d<0.
(Ⅲ)证明:由题意,设{cn}的公比为q,
则c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1).
因为{cn}为{an}的一个m项子列,
所以q为正有理数,且q<1,c1=
≤1 (a∈N*).
设q=
(K,L∈N*,且K,L互质,L≥2).
当K=1时,
因为q=
≤
,
所以c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1)≤1+
+(
)2+…+(
)m-1=2-(
)m-1,
所以c1+c2+c 3+…+cm≤2-(
)m-1.
当K≠1时,
因为cm=c1qm-1=
×
是{an}中的项,且K,L互质,
所以a=Km-1×M(M∈N*),
所以c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1)=
(
+
+
+…+
).
因为L≥2,K,M∈N*,
所以c1+c2+c 3+…+cm≤1+
+(
)2+…+(
)m-1=2-(
)m-1.
综上,c1+c2+c 3+…+cm≤2-
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
(Ⅱ)证明:由题意,知1≥b1>b2>b3>b4>b5>0,
所以d=b2-b1<0.
假设b1=1,
由{bn}为{an}的一个5项子列,得b2≤
| 1 |
| 2 |
所以d=b2-b1≤
| 1 |
| 2 |
| 1 |
| 2 |
因为b5=b1+4d,b5>0,
所以4d=b5-b1=b5-1>-1,即d>-
| 1 |
| 4 |
这与d≤-
| 1 |
| 2 |
所以假设不成立,即b1≠1.
所以b1≤
| 1 |
| 2 |
因为b5=b1+4d,b5>0,
所以4d=b5-b1≥b5-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
综上,得-
| 1 |
| 8 |
(Ⅲ)证明:由题意,设{cn}的公比为q,
则c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1).
因为{cn}为{an}的一个m项子列,
所以q为正有理数,且q<1,c1=
| 1 |
| a |
设q=
| K |
| L |
当K=1时,
因为q=
| 1 |
| L |
| 1 |
| 2 |
所以c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1)≤1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以c1+c2+c 3+…+cm≤2-(
| 1 |
| 2 |
当K≠1时,
因为cm=c1qm-1=
| 1 |
| a |
| Km-1 |
| Lm-1 |
所以a=Km-1×M(M∈N*),
所以c1+c2+c 3+…+cm=c1(1+q+q2+…+qm-1)=
| 1 |
| M |
| 1 |
| Km-1 |
| 1 |
| Km-2L |
| 1 |
| Km-3L2 |
| 1 |
| Lm-1 |
因为L≥2,K,M∈N*,
所以c1+c2+c 3+…+cm≤1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上,c1+c2+c 3+…+cm≤2-
| 1 |
| 2m-1 |
点评:本题考查了等差数列、等比数列、以及新定义问题,要求学生能准确理解题中的新定义并加以应用,在解题中用到了列举法、公式法、反证法和分类讨论思想,有难度,属于难题.

练习册系列答案
相关题目
已知角α终边上异于原点一点P且|PO|=r,则P点坐标为( )
| A、P(sinα,cosα) |
| B、P(cosα,sinα) |
| C、P(rsinα,rcosα) |
| D、P(rcosα,rsinα) |
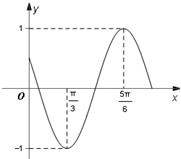 已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<
已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<
