题目内容
△ABC的三个内角A，B，C对应边分别为a，b，c．若A，B，C成等差数列，求证：
+
=1．
| c |
| a+b |
| a |
| b+c |
考点：等差数列的性质
专题：证明题,等差数列与等比数列
分析：利用A，B，C成等差数列，可得B=60°，利用余弦定理可得a2+c2=b2+ac，代入求解，即可证明结论．
解答：
证明：在△ABC中，∵A，B，C成等差数列，
∴B=60°，
∴b2=a2+c2-2accosB=a2+c2-ac，
∴a2+c2=b2+ac，
∴
+
=
=
=1．
∴B=60°，
∴b2=a2+c2-2accosB=a2+c2-ac，
∴a2+c2=b2+ac，
∴
| c |
| a+b |
| a |
| b+c |
| bc+c2+a2+ab |
| (a+b)(b+c) |
| bc+ab+b2+ac |
| ab+ac+b2+bc |
点评：利用等差数列的性质确定B，正确运用余弦定理是解题的突破口．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
角α顶点在坐标原点O，始边与x轴的非负半轴重合，tanα=-2，点P在α的终边上，点Q（-3，-4），则
与
夹角余弦值为（ ）
| OP |
| OQ |
A、-
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
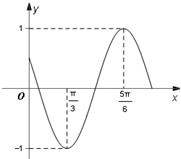已知函数f（x）=cos（ωx+φ）（ω＞0，0＜φ＜
