题目内容
抛物线的顶点在坐标原点,且以椭圆
+
=1的右顶点为焦点,则此抛物线的方程为 .
| x2 |
| 8 |
| y2 |
| 5 |
考点:抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出抛物线的焦点为F(2
,0),由此能求出抛物线的方程.
| 2 |
解答:
解:∵椭圆
+
=1的右顶点是F(2
,0),
抛物线的顶点在坐标原点,且以椭圆
+
=1的右顶点为焦点
∴抛物线的焦点为F(2
,0),
设抛物线方程为y2=2px,p>0,
则
=2
,p=4
,
∴此抛物线的方程为y2=8
x.
故答案为:y2=8
x.
| x2 |
| 8 |
| y2 |
| 5 |
| 2 |
抛物线的顶点在坐标原点,且以椭圆
| x2 |
| 8 |
| y2 |
| 5 |
∴抛物线的焦点为F(2
| 2 |
设抛物线方程为y2=2px,p>0,
则
| p |
| 2 |
| 2 |
| 2 |
∴此抛物线的方程为y2=8
| 2 |
故答案为:y2=8
| 2 |
点评:本题考查抛物线的标准方程的求法,是基础题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
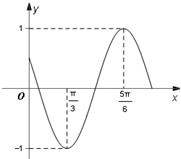 已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<
已知函数f(x)=cos(ωx+φ)(ω>0,0<φ<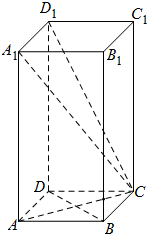 已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.
已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.