题目内容
在△ABC中,已知c=10,A=30°,C=120°,
(1)求a;
(2)求△ABC的面积.
(1)求a;
(2)求△ABC的面积.
考点:正弦定理
专题:解三角形
分析:在△ABC中,由正弦定理可得c的值,再根据△ABC的面积 S=
ab•sinC 运算求得结果.
| 1 |
| 2 |
解答:
解:∵在△ABC中,已知c=10,A=30°,C=120°,由正弦定理可得 a=
=
=
,
△ABC的面积 S=
ac•sinB=
×
×10×
=
.
| csinA |
| sinC |
10×
| ||||
|
| 10 |
| 3 |
| 3 |
△ABC的面积 S=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 3 |
| 1 |
| 2 |
| 25 |
| 3 |
| 3 |
点评:本题主要考查正弦定理,三角形的面积公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线y=kx-2与椭圆x2+4y2=80相交于不同的两点P、Q,若PQ的中点横坐标为2,则直线的斜率等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
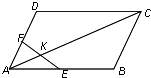 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,