题目内容
函数y=x-2sinx在[0，π]上的递增区间是 ．
考点：利用导数研究函数的单调性
专题：函数的性质及应用
分析：先对函数y=x-2sinx求导，令导数为0得f′（
）=0，在[0，
]与[
，π]上探讨导函数的正负．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：y′=1-2cosx，由y′=0解得x=
，
当0≤x＜
时，1-2cosx＜0，
∴函数y=x-2sinx在[0，
]上递减；
当
＜x≤π时，1-2cosx＞0，
∴函数y=x-2sinx在[
，π]上递增；
故答案为：[
，π]．
| π |
| 3 |
当0≤x＜
| π |
| 3 |
∴函数y=x-2sinx在[0，
| π |
| 3 |
当
| π |
| 3 |
∴函数y=x-2sinx在[
| π |
| 3 |
故答案为：[
| π |
| 3 |
点评：本题主要考查利用导数研究函数的单调性，导数的正负与函数单调区间之间的关系是解题的关键，属于基本题．
练习册系列答案
高中必刷题系列答案
相关题目
如图是一个圆锥的三视图，则其侧面积是（ ）
| A、π | B、2π | C、3π | D、4π |
如图是调查某地某公司1000名员工的月收入后制作的直方图．根据直方图估计：
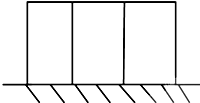用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍，且鸡舍内用相同的篱笆隔成三间（如图所示），如果挨着墙的边长为x，鸡舍面积为y（1）请把y表示成x的函数；
（2）当x为何值时，函数取最大值，并求出最大值．
已知圆C：（x-1）2+（y-2）2=25，直线l：（2m+1）x+（m+1）y-7m-4=0，m∈R，当直线l被圆C截得的弦长最短时的m的值是（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
已知数列{an}为等差数列，Sn是数列{an}的前n项和，a1+a6+a11=4π，则sin（S11）的值为（ ）
A、
| ||||
B、±
| ||||
C、
| ||||
D、-
|