题目内容
设a=log2tan70°，b=log2sin25°，c=log2cos25°，则它们的大小关系为（ ）
| A、a＜c＜b |
| B、b＜c＜a |
| C、a＜b＜c |
| D、b＜a＜c |
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用三角函数的单调性、对数函数的单调性即可得出．
解答：
解：∵tan70°＞tan45°=1，1＞cos25°=sin65°＞sin25°＞0，
∴a=log2tan70°＞c=log2cos25°＞b=log2sin25°，
∴a＞c＞b．
故选：B．
∴a=log2tan70°＞c=log2cos25°＞b=log2sin25°，
∴a＞c＞b．
故选：B．
点评：本题考查了三角函数的单调性、对数函数的单调性，属于基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若函数f（x）=
，则f（6）等于（ ）
| x+3 |
| A、3 | ||
| B、6 | ||
| C、9 | ||
D、
|
已知f（x）=
，若a=f（lg5），b=f（lg0.2）则下列正确的是（ ）
| 1+sin2x |
| 2 |
| A、a+b=0 |
| B、a-b=0 |
| C、a+b=1 |
| D、a-b=1 |
若θ是第二象限角，则（ ）
A、sin
| ||
B、cos
| ||
C、tan
| ||
D、cot
|
函数f（x）=loga（x）在其定义域上是（ ）
| A、增函数 | B、减函数 |
| C、不是单调函数 | D、单调性与a有关 |
若函数f（sinx）=cos2x，则f（cos15°）的值为（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
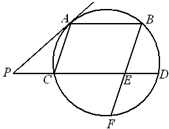如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．