题目内容
已知角α的终边上一点（1，1）
（1）求tanα的值；
（2）化简求值
．
（1）求tanα的值；
（2）化简求值
| 4sinα+2cosα |
| 5cosα+3sinα |
考点：任意角的三角函数的定义,同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：（1）利用正切函数的定义，可求tanα的值；
（2）弦化切，利用（1）的结论可求．
（2）弦化切，利用（1）的结论可求．
解答：
解：（1）∵角α的终边上一点（1，1），
∴tanα=1；
（2）∵tanα=1
∴
=
=
．
∴tanα=1；
（2）∵tanα=1
∴
| 4sinα+2cosα |
| 5cosα+3sinα |
| 4tanα+2 |
| 5+3tanα |
| 3 |
| 4 |
点评：本题考查任意角的三角函数的定义、同角三角函数基本关系的运用，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
计算sin43°cos13°-sin13°sin47°的值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若θ是第二象限角，则（ ）
A、sin
| ||
B、cos
| ||
C、tan
| ||
D、cot
|
若函数f（sinx）=cos2x，则f（cos15°）的值为（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
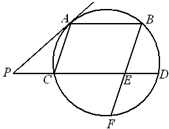如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．