题目内容
已知数列{an}(n∈N•)的前n项和为Sn,数列{
}是首项为0,公差为
的等差数列.
(1)求数列{an}的通项公式;
(2)设bn=
•(-2) an(n∈N•),对任意的正整数k,将集合{b2k-1,b2k,b2k+1}中的三个元素排成一个递增的等差数列,其公差为dx,求数列{dk}的通项公式.
(3)对(2)中的{dk}的前n项和Tn.
| Sn |
| n |
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)设bn=
| 4 |
| 15 |
(3)对(2)中的{dk}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得
=0+(n-1)•
=
(n-1)求出an=n-1.
(2)由(1)可知,bn=
•(-2)n-1,求出b2k,b2k-1,b2k+1由已知列出方程求出公差{dk}的通项公式.
(3)由(2)得数列{dk}为等比数列,由等比数列的前n项和公式得Tn=
(4n-1)
| Sn |
| n |
| 1 |
| 2 |
| n |
| 2 |
(2)由(1)可知,bn=
| 4 |
| 15 |
(3)由(2)得数列{dk}为等比数列,由等比数列的前n项和公式得Tn=
| 4 |
| 15 |
解答:
解:(1)由已知得
=0+(n-1)•
=
(n-1),
∴an=n-1
(2)由(1)可知,
bn=
•(-2)n-1,
∴b2k-1=
(-2)2k-2=
•22k-2,b2k=
(-2)2k-1
b2k=-
•22k-1
,b2k+1=
(-2)2k=
•22k
由2b2k-1=bk+bk+1及b2k<b2k-1<b2k+1
得b2k,b2k-1,b2k+1依次成递增的等差数列,
∴dk=b2k+1-b2k-1=
,
(3)由(2)得
=
=4,
∴数列{dk}为等比数列,
∴Tn=
=
(4n-1)
| Sn |
| n |
| 1 |
| 2 |
| n |
| 2 |
∴an=n-1
(2)由(1)可知,
bn=
| 4 |
| 15 |
∴b2k-1=
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
b2k=-
| 4 |
| 15 |
,b2k+1=
| 4 |
| 15 |
| 4 |
| 15 |
由2b2k-1=bk+bk+1及b2k<b2k-1<b2k+1
得b2k,b2k-1,b2k+1依次成递增的等差数列,
∴dk=b2k+1-b2k-1=
| 4k |
| 5 |
(3)由(2)得
| dk+1 |
| dk |
| ||
|
∴数列{dk}为等比数列,
∴Tn=
| ||||
| 1-4 |
=
| 4 |
| 15 |
点评:本题考查数列通项公式的求法、数列的前n项和公式的求法;等差、等比数列是两个基本数列.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
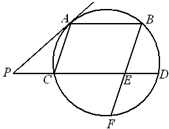 如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.