题目内容

有甲乙丙丁4个人过一座简易木桥，这四个人过桥分别所用的时间是2分钟，4分钟，6钟，8分钟，由于木桥质量原因，桥上最多只能有两个人． 请你设置一个方案，使这4个人在最快的时间过桥，写清步骤，最后算出所需时间．
考点：排序问题与算法的多样性
专题：操作型,算法和程序框图
分析：根据要求出四个人过桥最少时间，即可得出应首先让用时最少的两人先过桥．
解答： 解：方法不唯一：
1．甲乙先上桥；
2.2分钟后甲过了桥同时丁上桥；
3．再过2分钟后乙过了桥同时丙上桥；
4.6分钟后丙丁同时上岸．
∴所需时间是2+2+6=10（分钟）．
点评：此题主要考查了应用类问题，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
复数Z=x+yi（xy∈R）满足|Z-4i|=|Z+2|，则2x+4y的最小值为（　　）
A、2
B、4
C、8
2
D、4
2
若函数f（sinx）=cos2x，则f（cos15°）的值为（　　）
A、
1
2
B、-
1
2
C、-
3
2
D、
3
2
设函数f（x）=cos2x+2
3
sinxcosx（x∈R）的最大值为M，最小正周期为T．
（1）求M，T的值．
（2）20个互不相等的正数xi满足f（xi）=
3
2
M，且xi＜10π（i=1，2，…，20），求x1+x2+…+x20的值．
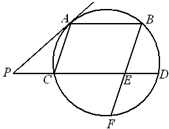如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．
（Ⅰ）求AC的长；
（Ⅱ）试比较BE与EF的长度关系．
数列{an}的首项a1=a，an+an+1=3n-54，n∈N*
（1）求数列{an}的通项公式；
（3）设{an}的前n项和为Sn，若Sn的最小值为-243，求a的取值范围？
已知圆C1的方程为x2+（y-2）2=1，定直线l的方程为y=-1．动圆C与圆C1外切，且与直线l相切．
（1）求动圆圆心C的轨迹M的方程；
（2）直线l′与轨迹M相切于第一象限的点P，过点P作直线l′的垂线恰好经过点A（0，6），并交轨迹M于异于点P的点Q，求直线PQ的方程及弦|PQ|的长．
（1）已知sinα=
3
2
，α∈（
π
2
，π），求cosα，tanα．
（2）已知cosα=-
4
5
，求sinα，tanα．
若函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
π
2
）的最小值为-2，且它的图象经过点（0，
3
）和（
5π
6
，0）．
（1）写出一个满足条件的函数解析式f（x）；
（2）若函数f（x）在（0，
π
8
]上单调递增，求此函数所有可能的解析式；
（3）若函数f（x）在[0，2]上恰有一个最大值和最小值，求ω的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网