题目内容
18.在△ABC中,a,b,c分别是角A,B,C的对边,向量$\overrightarrow{m}$=(cos(A-B),sin(A-B)),$\overrightarrow{n}$=(cosB,-sinB),且 $\overrightarrow{m}$•$\overrightarrow{n}$=-$\frac{3}{5}$.(Ⅰ)求sinA的值;
(Ⅱ)若a=4$\sqrt{2}$,b=5,求角B的大小及向量$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影.
分析 (Ⅰ)由平面向量数量积的运算可得cos(A-B)cosB-sin(A-B)sinB=-$\frac{3}{5}$,得cosA的值,结合范围0<A<π,利用同角三角函数基本关系式可求sinA的值.
(Ⅱ)由正弦定理sinB,进而可得B,由余弦定理解得c的值,利用平面向量数量积的运算即可计算得解.
解答 (本题满分为12分)
解:(Ⅰ)由 $\overrightarrow{m}$•$\overrightarrow{n}$=-$\frac{3}{5}$,得cos(A-B)cosB-sin(A-B)sinB=-$\frac{3}{5}$,得cosA=-$\frac{3}{5}$;
又0<A<π,
所以sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$. …(5分)
(Ⅱ)由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,得sinB=$\frac{\sqrt{2}}{2}$,得B=$\frac{π}{4}$;
由余弦定理得a2=b2+c2-2bccosA,即(4$\sqrt{2}$)2=52+c2-2×5×c×(-$\frac{3}{5}$),
解得c=1或c=-7(舍去);
所以向量$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影值为$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$=-ccosB=-$\frac{\sqrt{2}}{2}$. …(12分)
点评 本题主要考查了平面向量数量积的运算,同角三角函数基本关系式,正弦定理,余弦定理在解三角形中的综合应用,属于基础题.

练习册系列答案
相关题目
9.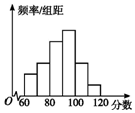 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )| A. | 32 | B. | 27 | C. | 24 | D. | 33 |
10.已知点A是抛物线x2=4y的对称轴与准线的交点,点F为抛物线的焦点,P在抛物线上且满足|PA|=m|PF|,当m取最大值时|PA|的值为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |