题目内容
2．在棱长为3的正方体ABCD-A1B1C1D1内部随机取一个点M，则点M到顶点A的距离超过1的概率为$1-\frac{π}{162}$．分析 由题意可得，点A距离等于a的点的轨迹是一个八分之一个球面，求出其体积，再根据几何概型概率公式结合正方体的体积的方法求解即可
解答 
解：由由题意可得正方形的体积为33=27
与点A距离等于1的点的轨迹是半径为1的一个八分之一个球面，
体积为$\frac{1}{8}×\frac{4}{3}π=\frac{π}{6}$
则点P到点A的距离超过1的概率为：1-$\frac{\frac{π}{6}}{27}$=1-$\frac{π}{162}$；
故答案为：1-$\frac{π}{162}$．
点评 本小题主要考查几何概型、几何概型的应用、几何体的体积等基础知识，考查空间想象能力、化归与转化思想．
练习册系列答案
相关题目
10．已知点A是抛物线x2=4y的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上且满足|PA|=m|PF|，当m取最大值时|PA|的值为（ ）
| A． | 1 | B． | $\sqrt{5}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{2}$ |
17．
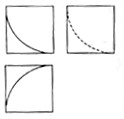如图所示，某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1，圆心角为90°的圆弧，则该几何体的体积是（ ）
如图所示，某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1，圆心角为90°的圆弧，则该几何体的体积是（ ）| A． | 1-$\frac{π}{12}$ | B． | 1-$\frac{π}{3}$ | C． | 1-$\frac{π}{6}$ | D． | 1-$\frac{π}{24}$ |
14．若变量x，y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-3≥0\end{array}\right.$，则xy的取值范围是（ ）
| A． | [0，5] | B． | $[{5，\frac{35}{4}}]$ | C． | $[{0，\frac{35}{4}}]$ | D． | [6，9] |
