题目内容
20.已知非负实数a,b,c满足ab+bc+ca=1,求证:$\frac{1}{a+b}$$+\frac{1}{b+c}$$+\frac{1}{c+a}$$≥\frac{5}{2}$.分析 设a≤b≤c,令f(a,b,c)=$\frac{1}{a+b}$$+\frac{1}{b+c}$$+\frac{1}{c+a}$,构造函数f(0,a+b,$\frac{1}{a+b}$)=$\frac{1}{a+b}$+$\frac{1}{a+b+\frac{1}{a+b}}$+a+b.利用函数思想转化换元利用基本不等式的性质即可证明.
解答 解:设a≤b≤c,令f(a,b,c)=$\frac{1}{a+b}$$+\frac{1}{b+c}$$+\frac{1}{c+a}$,
则 f(0,a+b,$\frac{1}{a+b}$)=$\frac{1}{a+b}$+$\frac{1}{a+b+\frac{1}{a+b}}$+a+b.
那么f(a,b,c)-f(0,a+b,$\frac{1}{a+b}$)=$\frac{1}{b+c}$$+\frac{1}{c+a}$--$\frac{1}{a+b+\frac{1}{a+b}}$--(a+b).(1)
又∵ab+bc+ca=1,
∴c=$\frac{1-ab}{a+b}$,(2)
把(2)代入(1)得:f(a,b,c)-f(0,a+b,$\frac{1}{a+b}$)=$\frac{a+b}{{a}^{2}+1}$+$\frac{a+b}{{b}^{2}+1}$-(a+b)-$\frac{a+b}{(a+b)^{2}+1}$
=(a+b)$[\frac{1}{{a}^{2}+1}+\frac{1}{{b}^{2}+1}$-1-$\frac{1}{(a+b)^{2}+1}]$
=(a+b)$\frac{2ab(1-ab)-{a}^{2}{b}^{2}(a+b)^{2}}{({a}^{2}+1)({b}^{2}+1)[(a+b)^{2}+1]}$
=(a+b)$\frac{2ab(a+b)c-{a}^{2}{b}^{2}(a+b)^{2}}{({a}^{2}+1)({b}^{2}+1)[(a+b)^{2}+1]}$
=$\frac{ab(a+b)^{2}[2c-ab(a+b)]}{({a}^{2}+1)({b}^{2}+1)[(a+b)^{2}+1]}$.
0≤a≤b≤c≤1,∴0≤a+b≤2,ab≤ac≤c(∵a≤1),
从而ab≤c,∴ab(a+b)≤2c,∴2c-ab(a+b)≥0.
从而f(a,b,c)-f(0,a+b,$\frac{1}{a+b}$)≥0,
∴f(a,b,c)≥f(0,a+b,$\frac{1}{a+b}$).
而$\frac{1}{a+b}$+a+b≥2.
f(0,a+b,$\frac{1}{a+b}$)=$\frac{1}{a+b}$+$\frac{1}{a+b+\frac{1}{a+b}}$+a+b.
而f(x)=x+1/x在[√2,+∞)上单调递增.
∴f(0,a+b,$\frac{1}{a+b}$)≥$2+\frac{1}{2}$=$\frac{5}{2}$.
∴f(a,b,c)≥f(0,a+b,$\frac{1}{a+b}$)≥$\frac{5}{2}$.
点评 本题考查了基本不等式的性质、函数的单调性、换元法,考查了推理能力与计算能力,属于难题.

 高中必刷题系列答案
高中必刷题系列答案| A. | (x-1)2+(y+1)2=9 | B. | (x-1)2+(y+1)2=3 | C. | (x+1)2+(y-1)2=9 | D. | (x+1)2+(y-1)2=3 |
| A. | P(X=0) | B. | P(X≤2) | C. | P(X=1) | D. | P(X=2) |
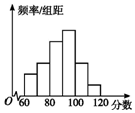 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )| A. | 32 | B. | 27 | C. | 24 | D. | 33 |
| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
