题目内容
不等式|3x-1|≤2的解集为 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：去绝对值将不等式转化为-2≤3x-1≤2，解出即可．
解答：
解：∵|3x-1|≤2，
∴-2≤3x-1≤2，
∴-1≤3x≤3，
∴-
≤x≤1，
故答案为：[-
，1]．
∴-2≤3x-1≤2，
∴-1≤3x≤3，
∴-
| 1 |
| 3 |
故答案为：[-
| 1 |
| 3 |
点评：本题考查了绝对值不等式的解法，是一道基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
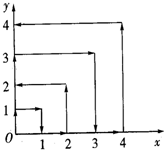如图，一个质点从原点出发，在与y轴．x轴平行的方向按（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→（2，2）…的规律向前移动，且每秒钟移动一个单位长度，那么到第2011秒时，这个质点所处位置的坐标是（ ）| A、（13，44） |
| B、（14，44） |
| C、（44，13） |
| D、（44，14） |
已知sin2α=
，则sin2（α+
）=（ ）
| 2 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知三次函数f（x）=
ax3-x2+x在（0，+∞）存在极大值点，则a的范围是（ ）
| 1 |
| 3 |
| A、（0，1） |
| B、（0，1] |
| C、（-∞，0） |
| D、（-∞，0）∪（0，1） |