题目内容
| ∫ | 1 0 |
考点:定积分
专题:导数的概念及应用
分析:只须根据定积分的定义先求出被积函数的原函数,然后求解即可.
解答:
解:
(x2-2k)dx=(
x3-2kx)|
=
-2k=1,
解得k=-
故答案为:-
| ∫ | 1 0 |
| 1 |
| 3 |
1 0 |
| 1 |
| 3 |
解得k=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题考查定积分的运算性质及微积分基本定理,熟记微积分基本定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
与双曲线x2-
=1有共同渐近线,且过点(2,
)的双曲线方程是( )
| y2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设某中学的学生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),可得回归方程为
=0.85x-85.71,则下列结论中不正确的是( )
 |
| y |
| A、y与x具有正的线性相关关系 | ||||
B、回归直线过样本点的中心(
| ||||
| C、若该中学某学生身高增加1cm,则其体重约增加0.85kg | ||||
| D、若该中学某学生身高为170 cm,则可断定其体重必为58.79kg |
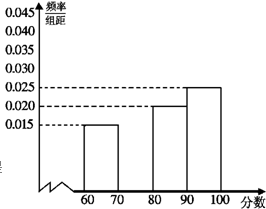 某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:
某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表: