题目内容
已知向量
=(2cosφ,2sinφ),φ∈(90°,180°),
=(1,1),则向量
与
的夹角为 .
| a |
| b |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:由条件计算出|
|、|
|、
•
的值,代入cosθ=
化简,结合θ、φ的范围,利用诱导公式求得θ的值.
| a |
| b |
| a |
| b |
| ||||
|
|
解答:
解:由题意可得|
|=2,|
|=
,
•
=2cosφ+2sinφ=2
sin(φ+45°),
设向量
与
的夹角为θ,则cosθ=
=
=sin(φ+45°)=cos(φ+45°-90°),
再结合θ∈[0°,180°],φ∈(90°,180°),可得θ=φ+45°-90°=φ-45°,
故答案为:φ-45°.
| a |
| b |
| 2 |
| a |
| b |
| 2 |
设向量
| a |
| b |
| ||||
|
|
2
| ||||
2
|
再结合θ∈[0°,180°],φ∈(90°,180°),可得θ=φ+45°-90°=φ-45°,
故答案为:φ-45°.
点评:本题考查的知识点是平面向量数量积的坐标表示、模、夹角,其中利用cosθ=
计算两个向量的夹角是解答本题的关键,属于基础题.
| ||||
|
|

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
在x轴、y轴上截距相等且与圆(x+2
)2+(y-3
)2=1相切的直线L共有( )条.
| 2 |
| 2 |
| A、2 | B、3 | C、4 | D、6 |
两台相互独立工作的电脑产生故障的概率分别为a,b,则产生故障的电脑台数均值为( )
| A、ab | B、a+b |
| C、1-ab | D、1-a-b |
设命题p:
=(3,1),
=(m,2)且
∥
;命题q:关于x的函数y=(m2-5m-5)ax(a>0且a≠1)是指数函数,则命题p是命题q的( )
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
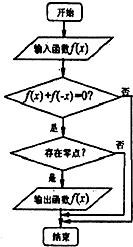 某程序框图如图所示,现依次输入如下四个函数:
某程序框图如图所示,现依次输入如下四个函数: