题目内容
已知函数f(x)=
,若方程f(x)=3x+a有且只有一个解,则实数a的取值范围是 .
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:画出函数图象,以及g(x)=3x+a的图象,从图象直观的找出有一个交点的自变量范围.
解答:
解:如图,

要使方程f(x)=3x+a有且只有一个解,只要函数f(x)的图象与g(x)=3x+a的图象只有一个交点即可,由图知,只要a≥4,或a<1即可.
故答案为:a≥4,或a<1.

要使方程f(x)=3x+a有且只有一个解,只要函数f(x)的图象与g(x)=3x+a的图象只有一个交点即可,由图知,只要a≥4,或a<1即可.
故答案为:a≥4,或a<1.
点评:本题考查了数形结合的方法求方程根的个数问题,关键是正确画图,视图.

练习册系列答案
相关题目
已知命题p:?x0∈R,x02+ax0+a<0.若?p是真命题,则实数a的取值范围是( )
| A、[0,4] |
| B、(0,4) |
| C、(-∞,0)∪(4,+∞) |
| D、(-∞,0]∪[4,+∞) |
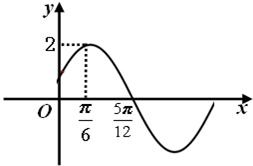 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<