题目内容
已知命题p:?x0∈R,x02+ax0+a<0.若?p是真命题,则实数a的取值范围是( )
| A、[0,4] |
| B、(0,4) |
| C、(-∞,0)∪(4,+∞) |
| D、(-∞,0]∪[4,+∞) |
考点:特称命题
专题:简易逻辑
分析:已知若命题p:?x0∈R,x02+ax0+a<0.?p是真命题,说明方程x2+ax+a≥0恒成立,根据判别式与根的关系进行求解;
解答:
解:∵若命题p:?x0∈R,x02+ax0+a<0.?p是真命题,说明方程x2+ax+a≥0恒成立,
∴△=a2-4a≤0,
解得0≤a≤4,
故选:A.
∴△=a2-4a≤0,
解得0≤a≤4,
故选:A.
点评:此题主要考查特称命题真假的判断以及一元二次方程根与判别式的关系,是一道基础题;

练习册系列答案
相关题目
下列函数中,是奇函数,又在定义域内为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=-x3 | ||
| D、y=x2 |
已知{an}是递增的等比数列a2=2,a4-
a3=-2,则此数列的公比q为( )
| 5 |
| 2 |
| A、3 | ||
| B、4 | ||
C、
| ||
| D、2 |
设偶函数f(x)=
sin(2x+φ)-cos(2x+φ)(|φ|<
),则( )
| 3 |
| π |
| 2 |
A、y=f(x)的对称中心为(
| ||||||
B、y=f(x)的对称中心为(
| ||||||
C、y=f(x)的对称中心为(
| ||||||
D、y=f(x)的对称中心为(
|
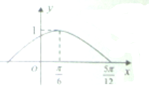 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-