题目内容
若函数为y=（sinx）4-（cosx）4，则导数为 ．
考点：简单复合函数的导数,二倍角的余弦
专题：导数的综合应用
分析：利用复合函数的导数运算法则、倍角公式、平方关系即可得出．
解答：
解：y′=4sin3xcosx-4cos3x（-sinx）=4sinxcosx（sin2x+cos2x）=2sin2x，
或y=sin2x-cos2x=-cos2x，y′=-2（-sin2x）=2sin2x．
故答案为：y′=2sin2x．
或y=sin2x-cos2x=-cos2x，y′=-2（-sin2x）=2sin2x．
故答案为：y′=2sin2x．
点评：本题考查了复合函数的导数运算法则、倍角公式、平方关系，属于基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
已知抛物线y2=4x与双曲线
-
=1（a＞0，b＞0）有相同的焦点F，点A，B是两曲线的交点，若（
+
）•
=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
在一次“爱眼日”活动中，随机抽取高三（1）班6名男生和6名女生的视力数据制成茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）：视力为5.0（含5.0）以上为正常视力，其他为近视眼．已知A、B、C为三个不共线的点，P为△ABC所在平面内一点，若
+
=
+
，则点P与△ABC的位置关系是（ ）
| PA |
| PB |
| PC |
| AB |
| A、点P在△ABC内部 |
| B、点P在△ABC外部 |
| C、点P在直线AB上 |
| D、点P在直线AC上 |
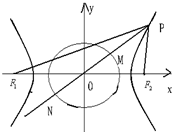如图F1，F2为双曲线C：