题目内容
直线y=3-x与坐标轴所围图形的面积为 .
考点:定积分在求面积中的应用
专题:计算题
分析:首先分别确定直线与x轴,y轴交点坐标,然后即可求出故直线y=-x+3与坐标轴围成三角形面积.
解答:
解:令x=0,得y=3,令y=0,得x=3,
则直线y=3-x与坐标轴交点坐标分别为(0,3),(3,0),
故直线y=3-x与坐标轴围成三角形面积为
×3×3=
.
故答案为:
.
则直线y=3-x与坐标轴交点坐标分别为(0,3),(3,0),
故直线y=3-x与坐标轴围成三角形面积为
| 1 |
| 2 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征.求出直线与坐标轴的交点,把求线段的长的问题转化为求函数的交点的问题.

练习册系列答案
相关题目
若函数f(x)=x3-3ax+3a在区间(0,2)内有极小值,则a的取值范围是( )
| A、a>0 | B、a>2 |
| C、0<a<2 | D、0<a<4 |
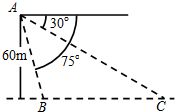 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )A、30(
| ||
B、120(
| ||
C、180(
| ||
D、240(
|
在△ABC中,角A、B、C的对边分别为a、b、c,点(a,b)在直线2xcosB-ycosC=ccosB上.
(1)求cosB的值;
(2)若a=
,b=2,求角A的大小及向量
在
方向上的投影.
(1)求cosB的值;
(2)若a=
2
| ||
| 3 |
| BC |
| BA |