题目内容
用0，1，3，5，7这五个数字，可以组成多少个没有重复数字且5不在十位位置上的五位数？
考点：计数原理的应用
专题：应用题,排列组合
分析：对0的位置，分类讨论，利用排列组合知识，即可得出结论．
解答：
解：0在十位位置的五位数，有
=120个；
0在除首位的其它位置的五位数，有
=54个，
故共有120+54=174个．
| A | 5 5 |
0在除首位的其它位置的五位数，有
| C | 1 3 |
| C | 1 3 |
| A | 3 3 |
故共有120+54=174个．
点评：本题考查计数原理的运用，考查学生的计算能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知直线l：y=x+3与双曲线
-
=1相交于A，B两点，线段AB中点为M，则OM的斜率为（ ）
| x2 |
| 9 |
| y2 |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在△ABC中，角A、B、C的对边分别为a、b、c，点（a，b）在直线2xcosB-ycosC=ccosB上．
（1）求cosB的值；
（2）若a=
，b=2，求角A的大小及向量
在
方向上的投影．
（1）求cosB的值；
（2）若a=
2
| ||
| 3 |
| BC |
| BA |
函数y=
的图象大致是（ ）
| x3 |
| 2x-1 |
A、 |
B、 |
C、 |
D、 |
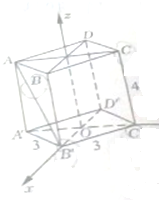已知长方体ABCD-A′B′C′D′的上，下底面都是边长为3的正方形，长方体的高为4，如图建立空间直角坐标系，求下列直线的一个方向向量．