题目内容
已知函数f(x)=|x-a|-2a+1(a∈R).
(Ⅰ)若a=1,解不等式f(x)<|x+1|;
(Ⅱ)若对任意x∈[1,2],f(x)≥0恒成立,求a的取值范围.
(Ⅰ)若a=1,解不等式f(x)<|x+1|;
(Ⅱ)若对任意x∈[1,2],f(x)≥0恒成立,求a的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(Ⅰ)由a=1,利用绝对值的意义求得不等式f(x)<|x+1|的解集.
(Ⅱ)由题意可得f(x)在[1,2]上的最小值大于或等于零,分类讨论求得f(x)在[1,2]上的最小值,从而求得a的取值范围.
(Ⅱ)由题意可得f(x)在[1,2]上的最小值大于或等于零,分类讨论求得f(x)在[1,2]上的最小值,从而求得a的取值范围.
解答:
解:(Ⅰ)当a=1,不等式f(x)<|x+1|即|x-1|-2+1<|x+1|,即|x-1|-|x+1|<1.
而|x-1|-|x+1|表示数轴上的x对应点到1对应点的距离减去它到-1对应点的距离,
而-
对应点到1对应点的距离减去它到-1对应点的距离正好等于1,故|x-1|-|x+1|<1的解集为{x|x>-
},
即原不等式的解集为{x|x>-
}.
(Ⅱ)若对任意x∈[1,2],①当a≤1时,函数f(x)=x-a-2a+1=x-3a+1,f(x)在[1,2]上单调递增,
f(x)的最小值为f(1)=2-3a,由2-3a≥0求得a≤
,
综合可得a≤
.
②当1<a<2时,f(x)=
,故f(x)在[1,a]上单调递减,在(a,1]上单调递增,
故f(x)的最小值为f(a)=1-2a,由1-2a≥0,求得a≤
,不满足前提条件1<a<2,故舍去.
③当a≥2时,函数f(x)=-x+a-2a+1=-a+1-x,f(x)在[1,2]上单调递减,
f(x)的最小值为f(2)=-1-a,由-1-a≥0求得a≤-1,不满足前提条件a≥2,故舍去.
综上可得,a≤
.
而|x-1|-|x+1|表示数轴上的x对应点到1对应点的距离减去它到-1对应点的距离,
而-
| 1 |
| 2 |
| 1 |
| 2 |
即原不等式的解集为{x|x>-
| 1 |
| 2 |
(Ⅱ)若对任意x∈[1,2],①当a≤1时,函数f(x)=x-a-2a+1=x-3a+1,f(x)在[1,2]上单调递增,
f(x)的最小值为f(1)=2-3a,由2-3a≥0求得a≤
| 2 |
| 3 |
综合可得a≤
| 2 |
| 3 |
②当1<a<2时,f(x)=
|
故f(x)的最小值为f(a)=1-2a,由1-2a≥0,求得a≤
| 1 |
| 2 |
③当a≥2时,函数f(x)=-x+a-2a+1=-a+1-x,f(x)在[1,2]上单调递减,
f(x)的最小值为f(2)=-1-a,由-1-a≥0求得a≤-1,不满足前提条件a≥2,故舍去.
综上可得,a≤
| 2 |
| 3 |
点评:本题主要考查绝对值的意义,函数的恒成立问题,利用单调性求函数在闭区间上的最值,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在[0,+∞)上的函数f(x)满足f(x+2)=f(x)+x,且当x∈[0,2)时,f(x)=x.则f(101)=( )
| A、2015 | B、2105 |
| C、2150 | D、2501 |
若函数f(x)=x3-3ax+3a在区间(0,2)内有极小值,则a的取值范围是( )
| A、a>0 | B、a>2 |
| C、0<a<2 | D、0<a<4 |
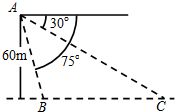 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于( )A、30(
| ||
B、120(
| ||
C、180(
| ||
D、240(
|