题目内容
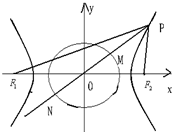如图F1，F2为双曲线C：| x2 |
| a2 |
| y2 |
| b2 |
| A、5 | B、30 | C、225 | D、15 |
考点：双曲线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：设P（m，n），代入双曲线的方程，设双曲线的离心率为e，由双曲线的第二定义可得，|PF1|=em+a，|PF2|=em-a，运用平方差公式以及圆的半径，化简整理，结合离心率公式和a，b，c的关系，计算即可得到所求值．
解答：
解：设P（m，n），则
-
=1，即有n2=b2（
-1），
设双曲线的离心率为e，由双曲线的第二定义可得，
|PF1|=em+a，|PF2|=em-a，
|PF1|•|PF2|=15，即为（em+a）（em-a）=15，
m2=
，
则|PM|•|PN|=（
-
）（
+
）
=（m2+n2）-（a2-b2）=
+b2•
•
-b2-a2+b2
=
（15+a2）-a2=15．
故选：D．
| m2 |
| a2 |
| n2 |
| b2 |
| m2 |
| a2 |
设双曲线的离心率为e，由双曲线的第二定义可得，
|PF1|=em+a，|PF2|=em-a，
|PF1|•|PF2|=15，即为（em+a）（em-a）=15，
m2=
| 15+a2 |
| e2 |
则|PM|•|PN|=（
| m2+n2 |
| a2-b2 |
| m2+n2 |
| a2-b2 |
=（m2+n2）-（a2-b2）=
| 15+a2 |
| e2 |
| 1 |
| a2 |
| 15+a2 |
| e2 |
=
| (a2+b2) | ||
a2•
|
故选：D．
点评：本题考查双曲线的定义、方程和性质，主要考查双曲线的第二定义的运用和离心率公式，考查化简整理的运算能力，属于中档题．
练习册系列答案
相关题目
若函数f（x）=x3-3ax+3a在区间（0，2）内有极小值，则a的取值范围是（ ）
| A、a＞0 | B、a＞2 |
| C、0＜a＜2 | D、0＜a＜4 |
设平面α∥平面β，直线a?α，点B∈β，则下列三个命题中为真命题的个数为（ ）
①在β内过点B的所有直线中存在唯一一条与a垂直的直线
②过直线a存在唯一一条与β垂直的平面
③在β内过点B的所有直线中存在唯一一条与a平行的直线．
①在β内过点B的所有直线中存在唯一一条与a垂直的直线
②过直线a存在唯一一条与β垂直的平面
③在β内过点B的所有直线中存在唯一一条与a平行的直线．
| A、0 | B、1 | C、2 | D、3 |
设集合M={x|x2≤4}，N={-1，0，4}，则M∩N=（ ）
| A、{-1，0，4} |
| B、{-1，0} |
| C、{0，4} |
| D、{-2，-1，0} |